Эмпирическая функция распределения. Эмпирической функцией распределения называется функция, которая каждому значению x ставит в соответствие относительную частоту события {X < x}

Эмпирической функцией распределения 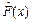называется функция, которая каждому значению x ставит в соответствие относительную частоту события { X < x } (обозначающего тот факт, что с.в. Х примет значение меньшее, чем х). Расчетная формула для вычисления 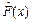имеет вид:

,

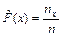где n – объём исследуемой выборки;

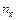– число элементов выборки, меньших данного фиксированного значения х.

Свойства эмпирической функции распределения:

1 Все возможные значения эмпирической функции распределения принадлежат отрезку [0, 1]: .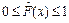

2 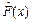– неубывающая функция своего аргумента, то есть 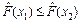для любых значений x ₁ и x ₂, таких, что .

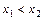3 Если все выборочные значения исследуемой случайной величины принадлежат отрезку [ a; b ], то 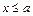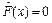при , при .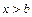

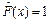Важнейшее свойство эмпирической функции распределения состоит в том, что при увеличении объема выборки n, значение этой функции в каждой точке приближается к значению теоретической функции распределения F (x) в указанной точке, т. е. эмпирическая функция распределения является экспериментальным аналогом (оценкой) неизвестной исследователю теоретической функции распределения.