Важнейшим этапом статистической обработки данных является вычисление оценок числовых характеристик исследуемой случайной величины. Полученные оценки позволяют в числовой форме описать характерные черты статистического распределения и являются базой для построения математической модели изучаемого случайного явления.
Любая функция 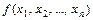 от результатов наблюдения
от результатов наблюдения 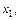
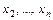 исследуемой с. в. X называется выборочной статистикой или просто статистикой. Статистика
исследуемой с. в. X называется выборочной статистикой или просто статистикой. Статистика 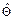 , используемая в качестве приближённого значения неизвестного параметра Q, называется статистической оценкой параметра Q.
, используемая в качестве приближённого значения неизвестного параметра Q, называется статистической оценкой параметра Q.
Существует два вида оценок параметров: точечные и интервальные. Точечные оценки определяют точку 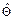 , являющуюся некоторым приближением оцениваемого параметра Q. Интервальная оценка представляет собой интервал
, являющуюся некоторым приближением оцениваемого параметра Q. Интервальная оценка представляет собой интервал 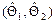 , который с заданной вероятностью накрывает неизвестное значение параметра Q.
, который с заданной вероятностью накрывает неизвестное значение параметра Q.
Познакомимся сначала с точечными оценками. Поскольку любая выборка является конечной и случайной, все выборочные функции 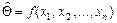 являются случайными величинами, то есть при переходе от одной выборки к другой вычисленные значения оценки
являются случайными величинами, то есть при переходе от одной выборки к другой вычисленные значения оценки 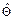 будут отличаться друг от друга. Желательно, чтобы получаемые значения
будут отличаться друг от друга. Желательно, чтобы получаемые значения 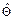 располагались как можно ближе к истинному значению оцениваемого параметра Q. Это достигается в тех случаях, когда статистическая оценка
располагались как можно ближе к истинному значению оцениваемого параметра Q. Это достигается в тех случаях, когда статистическая оценка 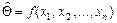 обладает такими свойствами, как состоятельность, несмещённость и эффективность.
обладает такими свойствами, как состоятельность, несмещённость и эффективность.
Статистическая оценка 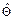 называется состоятельной, если ее вычисляемое по опытным данным значение при увеличении объема выборки сходится по вероятности к истинному значению
называется состоятельной, если ее вычисляемое по опытным данным значение при увеличении объема выборки сходится по вероятности к истинному значению 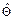 оцениваемого параметра, то есть, если для любого, сколь угодно малого
оцениваемого параметра, то есть, если для любого, сколь угодно малого 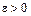
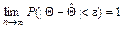 .
.
Оценка 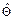 называется несмещенной (или оценкой без систематической ошибки), если ее математическое ожидание совпадает со значением
называется несмещенной (или оценкой без систематической ошибки), если ее математическое ожидание совпадает со значением 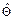 оцениваемого параметра:
оцениваемого параметра: 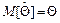 .
.
Несмещенная оценка 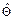 называется эффективной, если по сравнению с другими оценками параметра, вычисляемыми на основании выборок одинакового объема n, она обладает наименьшей дисперсией.
называется эффективной, если по сравнению с другими оценками параметра, вычисляемыми на основании выборок одинакового объема n, она обладает наименьшей дисперсией.
Ниже приведены формулы для вычисления точечных оценок случайной величины на основании имеющихся выборочных данных 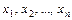 .
.
1 В качестве оценки математического ожидания (характеризующего среднее значение случайной величины) используется среднее арифметическое 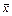 выборочных значений. Эта статистика называется выборочным средним
выборочных значений. Эта статистика называется выборочным средним
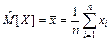 . (1)
. (1)
2 Для оценивания по выборочным данным моды распределения (т.е. наиболее вероятного значения 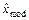 ), используется то значение случайной величины сгруппированного статистического ряда, которому соответствует наибольшее значение частоты. По интервальному статистическому ряду определяется модальный интервал, в который попало наибольшее число элементов выборки, и в качестве точечной оценки моды может использоваться середина этого интервала.
), используется то значение случайной величины сгруппированного статистического ряда, которому соответствует наибольшее значение частоты. По интервальному статистическому ряду определяется модальный интервал, в который попало наибольшее число элементов выборки, и в качестве точечной оценки моды может использоваться середина этого интервала.
3 Для определения выборочного значения медианы (средневероятного значения с. в.) используется вариационный ряд. В качестве оценки медианы 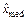 принимают средний член этого ряда, если значение n – нечётно, и среднее арифметическое двух средних членов этого ряда, если n – чётно.
принимают средний член этого ряда, если значение n – нечётно, и среднее арифметическое двух средних членов этого ряда, если n – чётно.
4 В качестве оценки дисперсии (являющейся мерой рассеивания значений случайной величины относительно ее среднего значения) используется статистика
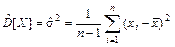 . (2)
. (2)
5 Оценка среднего квадратического отклонения
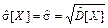 . (3)
. (3)
6 Оценка коэффициента асимметрии (представляющего собой меру «скошенности» распределения случайной величины относительно среднего значения)
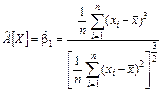 . (4)
. (4)
В пакете статистических программ STATGRAPHICS для вычисления оценки коэффициента асимметрии используется формула
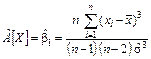 .
.
Для симметричных функций плотности распределений оценка 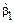 должна быть близка к нулю, в то время как для распределения, гистограмма которого имеет «длинную часть», расположенную справа от ее вершины,
должна быть близка к нулю, в то время как для распределения, гистограмма которого имеет «длинную часть», расположенную справа от ее вершины, 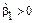 , а если слева – то
, а если слева – то 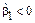 .
.
7 Оценка коэффициента эксцесса вычисляется по формуле
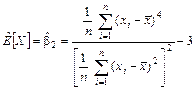 . (5)
. (5)
В пакете STATGRAPHICS оценка  вычисляется следующим образом:
вычисляется следующим образом:
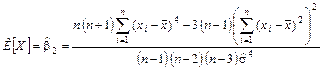 .
.
Коэффициент эксцесса характеризует островершинность распределения (поведение кривой распределения в районе ее модального значения).
Напомним, что своеобразным аналогом отсчета в измерении степени островершинности служит нормальное распределение, для которого теоретическое значение 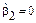 (
(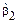 – близка к нулю). Для островершинного (по сравнению с нормальным) распределения –
– близка к нулю). Для островершинного (по сравнению с нормальным) распределения – 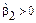 , а для плосковершинного –
, а для плосковершинного – 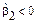 .
.
Замечание –Приведенные выше статистики 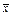 ,
, 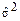 ,
, 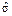
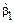 ,
, 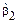 являются состоятельными и несмещенными оценками соответственно
являются состоятельными и несмещенными оценками соответственно 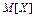 ,
, 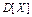 ,
, 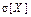 ,
, 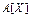 и
и 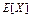 .
.
Пример 1 При изучении характеристик работы цеха в результате наблюдений получена выборка значений случайной величины X, число отказов оборудования в течение рабочей смены: 3, 1, 0, 1, 3, 6, 2, 2, 1, 1, 4, 4, 1, 4, 2, 0, 1, 5, 3, 2, 2, 1, 3, 1, 1, 4, 2, 1, 1, 3, 1, 2, 1, 0, 2, 1, 2, 0, 1, 1, 1, 4, 4, 2, 1, 4, 1, 2, 3, 2.
Задание: исследовать экспериментальные данные с целью изучения свойств случайной величины X.
Решение. 1 Построим вариационный ряд, соответствующий полученной выборке: 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5, 6.
2 Поскольку изучаемая случайная величина является дискретной, ее статистический закон распределения запишем в виде сгруппированного статистического ряда:
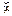 | |||||||
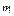 | |||||||
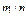 | 0,08 | 0,38 | 0,24 | 0,12 | 0,14 | 0,02 | 0,02 |
Столбцовая диаграмма, построенная на основании сгруппированного статистического ряда, изображена на рисунке 3.
3 Построим эмпирическую функцию распределения исследуемой случайной величины:
при x £ 0: 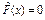 , т. к. нет ни одного наблюденного значения с.в., меньшего 0;
, т. к. нет ни одного наблюденного значения с.в., меньшего 0;
при 0 < x £ 1 только одно значение случайной величины 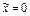 меньше рассматриваемых значений х, поэтому
меньше рассматриваемых значений х, поэтому 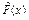 равна относительной частоте события { Х = 0};
равна относительной частоте события { Х = 0}; 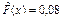 ;
;
при 1 < x £ 2 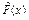 равна сумме относительных частот событий{ Х = 0} и{ Х = 1}:
равна сумме относительных частот событий{ Х = 0} и{ Х = 1}: 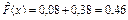 ;
;
при 2 < x £ 3: 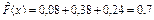 и т.д.
и т.д.
Таким образом:
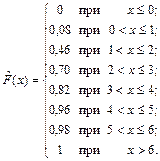
График функции 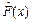 изображён на рисунке 4.
изображён на рисунке 4.
 Рисунок 3 – Столбцовая диаграмма (пример 1) Рисунок 3 – Столбцовая диаграмма (пример 1) | 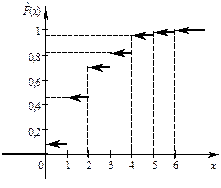 Рисунок 4 – График эмпирической функции распределения (пример 1) Рисунок 4 – График эмпирической функции распределения (пример 1) |
4 Вычислим точечные оценки числовых характеристик случайной величины X.
Оценка математического ожидания
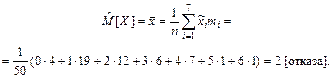
Оценка моды данной случайной величины равна 1 [отказ] (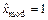 ), так как этому значению соответствует наибольшее значение частоты.
), так как этому значению соответствует наибольшее значение частоты.
Оценку медианы определим на основании вариационного ряда
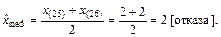
Оценка дисперсии
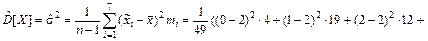
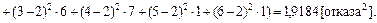
Оценка среднего квадратического отклонения
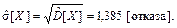
Оценки коэффициентов асимметрии и эксцесса:
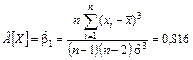 ;
;
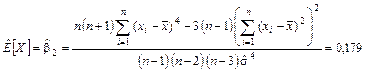 .
.
Выводы. Итак, мы выполнили анализ выборки значений дискретной случайной величины, характеризующей число отказов оборудования в течение рабочей смены. Объём выборки n = 50. Минимальное число отказов оборудования в течение рабочей смены равно 0, максимальное – 6. Среднее значение числа отказов равно 2; наиболее вероятное – 1, а средневероятное – 2. Среднеквадратическое отклонение числа отказов оборудования от среднего значения равно 1,385.
Пример 2 В процессе функционирования технического устройства, его параметры могут выходить из области допустимых значений. В этом случае необходимо производить переналадку устройства. Исследуемая случайная величина Х представляет собой продолжительность безотказной работы устройства (выраженную в часах) между двумя последовательными переналадками:
| 6,421; | 5,034; | 0,599; | 10,687; | 26,294; | 7,852; | 14,040; | 8,933; | 4,062; | 1,573; |
| 5,455; | 2,810; | 15,658; | 3,692; | 1,825; | 17,760; | 8,030; | 3,218; | 2,872; | 8,247; |
| 0,417; | 1,995; | 0,611; | 12,059; | 0,665; | 21,434; | 22,102; | 10,709; | 2,283; | 5,649; |
| 6,773; | 30,034; | 3,702; | 12,834; | 2,723; | 5,255; | 12,595; | 3,533; | 34,540; | 9,238; |
| 1,673; | 24,919; | 15,511; | 7,154; | 1,816; | 8,401; | 22,239; | 2,902; | 3,083; | 7,176. |
Задание: произвести первичную обработку полученных опытных данных с целью изучения свойств случайной величины Х.
Решение. 1 Построим вариационный ряд:
| 0,417; | 0,599; | 0,61; | 0,665; | 1,573; | 1,673; | 1,816; | 1,825; | 1,995; | 2,283; |
| 2,723; | 2,810; | 2,872; | 2,902; | 3,083; | 3,218; | 3,533; | 3,692; | 3,703; | 4,062; |
| 4,176; | 5,034; | 5,255; | 5,455; | 5,649; | 6,421; | 6,773; | 7,154; | 7,852; | 8,030; |
| 8,247; | 8,401; | 8,933; | 9,238; | 10,687; | 10,709; | 12,059; | 12,595; | 12,834; | 14,040; |
| 15,511; | 15,658; | 17,760; | 21,434; | 22,102; | 22,239; | 24,919; | 26,294; | 30,034; | 34,540. |
Статистический закон распределения данной непрерывной случайной величины представим в виде интервального статистического ряда.
Вычислим длину интервала:
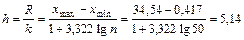 .
.
Определив границы интервалов разбиения (C 1 = x min – h /2 = 0,417 – 2,57 =
= –2,153, C 2 = C 1 + h = –2,153 + 5,14 = 2,987, C 3 = C 2 + h = 2,987 + 5,14 = 8,127 и т. д.), построим интервальный статистический ряд:
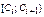 | [–2,153; 2,987) | [2,987; 8,127) | [8,127; 13,267) | [13,267; 18,407) | [18,407; 23,547) | [23,547; 28,687) | [28,687; 33,827) | [33,827; 38,967) |
 | 0,417 | 5,557 | 10,697 | 15,837 | 20,977 | 26,117 | 31,257 | 36,397 |
 | ||||||||
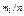 | 0,28 | 0,32 | 0,18 | 0,08 | 0,06 | 0,04 | 0,02 | 0,02 |
Для контроля убедимся, что 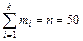 , , 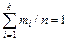 . Графическое изображение интервального статистического ряда приведено на рисунке 5. 2 Для приближённого построения эмпирической функции распределения воспользуемся соотношением . Графическое изображение интервального статистического ряда приведено на рисунке 5. 2 Для приближённого построения эмпирической функции распределения воспользуемся соотношением 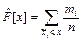 *: *: | 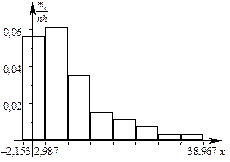 Рисунок 5 – Гистограмма относительных частот (пример 2) Рисунок 5 – Гистограмма относительных частот (пример 2) |
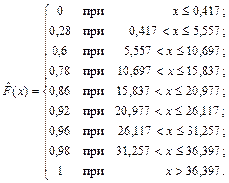
График полученной таким образом эмпирической функции распределения приведён на рисунке 6, а.
| а) | б) |
 | 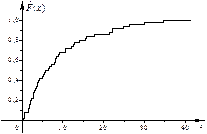 |
| Рисунок 6 – График эмпирической функции распределения (пример 2) |
На рисунке 6, б приведён график эмпирической функции распределения данной случайной величины, построенный при использовании всего набора имеющихся экспериментальных данных.
Вычислим точечные оценки числовых характеристик случайной величины, обозначающей продолжительность безотказной работы устройства между двумя последовательными переналадками:
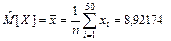 [ч];
[ч];
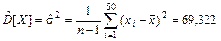 [ч2];
[ч2];
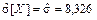 [ч];
[ч];
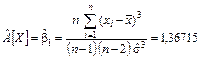 ;
;
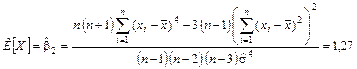 .
.
В качестве оценки моды можно принять среднее значение модального интервала [2,987; 8,127): 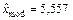 ч.
ч.
В качестве оценки медианы примем среднее значение между 25-м и 26-м элементами вариационного ряда: 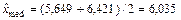 ч.
ч.
Выводы. В результате исследования выборки значений непрерывной случайной величины, характеризующей время безотказной работы устройства между двумя последовательными переналадками, получили следующие результаты, ч: минимальное время безотказного функционирования – 0,417, максимальное – 34,54, среднее значение времени безотказного функционирования устройства – 8,922, наиболее вероятное значение – 5,557, средневероятное – 6,035. Среднеквадратическое отклонение времени безотказного функционирования устройства от среднего значения – 8,326. Оценка коэффициента асимметрии – 1,367, оценка коэффициента эксцесса – 1,27.
 2015-04-08
2015-04-08 5224
5224
