Общепрофессиональная дисциплина: Электродинамика. Электродинамик сплошных сред.
Уравнения Максвелла, материальные уравнения, граничные условия для электрического и магнитного полей.
Уравнения Максвелла являются обобщением эмпирических законов для электрического и магнитного полей и гипотезы Максвелла о токах смещения (рис. 1)
| № | В Гауссовой системе единиц: | В СИ: |
| I | 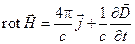 | 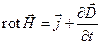 |
| II | 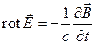 | 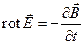 |
| III | 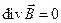 | 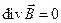 |
| IV | 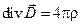 | 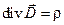 |
| V | 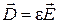 | 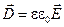 |
| VI | 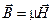 | 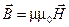 |
| VII | 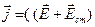 | 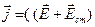 |
| VIII | 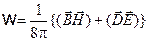 | 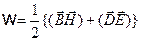 |
Таблица 1 – Уравнения Максвелла в Гауссовой и международной системах единиц
Обозначения в таблице: c = const = 3×108 м/с – электродинамическая постоянная в Гауссовой системе единиц (скорость света в вакууме)
В математическом смысле здесь 5 полей: 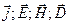 и
и 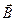 . Все они функции
. Все они функции 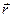 и t.
и t. 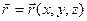 . Здесь r – объемная плотность неподвижных зарядов, j – плотность тока проводимости, (– удельная электропроводность, w – объемная плотность энергии электромагнитного поля.
. Здесь r – объемная плотность неподвижных зарядов, j – плотность тока проводимости, (– удельная электропроводность, w – объемная плотность энергии электромагнитного поля.
I уравнение Максвелла является следствием эмпирического закона Био-Савара-Лапласа, утверждающего, что вокруг проводника с током возникает магнитное поле, и вытекающей из него теоремы о циркуляции, к которой можно прийти, интегрируя уравнение I и применяя теорему Стокса
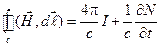 , где
, где
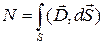
поток вектора индукции электрического поля через поверхность S.
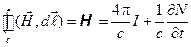 , (1.1)
, (1.1)
где H – магнитодвижущая сила. Физический смысл: вихревое магнитное поле возникает, при наличии токов проводимости или токов смещения. Последнее слагаемое в уравнении (1.1) является следствием дополнительного предположения Максвелла о том, что магнитное поле возникает не только вокруг тока проводимости (движущихся зарядов), но и вокруг силовых линий меняющегося со временем электрического поля – токов смещения (рис. 1), плотность которых определяется соотношением
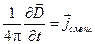 (1.2)
(1.2)
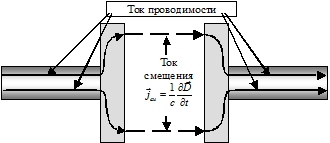
Рисунок 2 – гипотеза Максвелла о токах смещения
II уравнение Максвелла является следствием закона электромагнитной индукции, к которому можно прийти, интегрируя уравнение II и применяя теорему Стокса
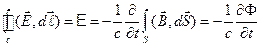 (1.3)
(1.3)
получаем
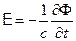
– ЭДС индукции (закон Фарадея). Физический смысл: вихревое электрическое поле возникает, при наличии меняющегося во времени магнитного поля.
III уравнение Максвелла является следствием безуспешности попыток, обнаружить экспериментально магнитные заряды (монополи). Интегрируя третье уравнение Максвелла по объему и применяем теорему Остроградского-Гаусса
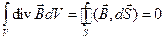 , (1.4)
, (1.4)
приходим к констатации замкнутости силовых линий магнитного поля.
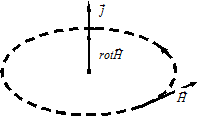
Рисунок 3 – Магнитное поле бывает только вихревым
IV уравнение Максвелла является следствием эмпирического закона закон Кулона, точнее, вытекающей из него электростатической теоремы Гаусса, к которой приходим, интегрируя четвертое уравнение Максвелла по объему и применяем теорему Остроградского-Гаусса
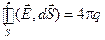 ,
, 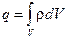 (1.5)
(1.5)
Уравнения V-VII – материальные уравнения – уравнения состояния вещества, характеризуемого диэлектрической проницаемостью e, магнитной проницаемостью m, и удельной проводимостью (
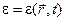
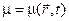
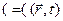 (1.6)
(1.6)
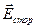 – напряженность поля сторонних сил – сил не электростатического происхождения.
– напряженность поля сторонних сил – сил не электростатического происхождения.
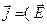 – закон Ома в дифференциальной форме.
– закон Ома в дифференциальной форме.
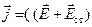
Уравнение VIII определяет плотность энергии электромагнитного поля
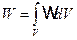 .
.
 2015-04-08
2015-04-08 2083
2083