Электродинамические потенциалы

Так как дивергенция ротора произвольного векторного поля равна нулю, то из III уравнения Максвелла следует существование векторного потенциала 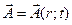, неявно определяемого соотношением

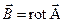. (4.1)

Подстановка этого соотношения во второе уравнение Максвелла

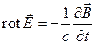
приводит к соотношению

.

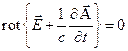Так как ротор градиента любого скалярного поля 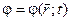равен нулю, то в самом общем случае последнее соотношение выполняется, если

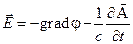(4.2)

Соотношение (4.1) в силу вышеупомянутого свойства определяет векторный потенциал 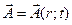неоднозначно, а с точностью до дающего нулевой вклад в (4.1) градиента произвольной скалярной функции y, т.е.

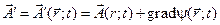. (4.3)

Подстановка этого соотношения в (4.2) дает

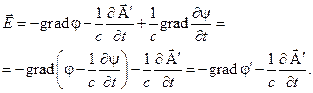
Т.е. неоднозначность (4.3) порождает неоднозначность

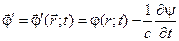(4.4)

Преобразования потенциалов (4.3) и (4.4) называются калибровочными преобразованиями, а произвольная функция 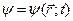– калибровочной функцией. Очевидно, что наблюдаемые поля 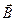и 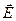инвариантны относительно калибровочных преобразований.