2015-04-08
201
Вычислить предел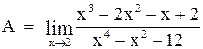 
.
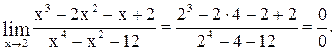
В числителе и знаменателе получаются нули за счет сомножителя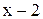 
, который стремится к нулю при 
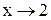. Разложим многочлены на множители, разделив их на
.
- 
- 
.
- 
- 
- 
- 
.
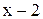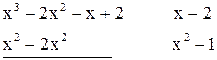
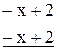
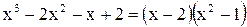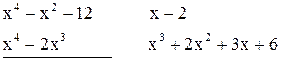
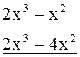
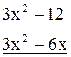
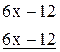
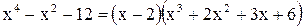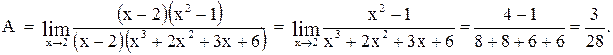
Замечание. При разложении многочлена в числителе можно было применить способ группировки и вынесения общего множителя, а в знаменателе найти корни, решив биквадратное уравнение.
Контрольные варианты к задаче 12
Вычислить пределы функций:
 .
|  .
|
 .
|  .
|
 .
|  .
|
 .
|  .
|
 .
 .
|  .
|
 .
| |
 .
|  .
|
 .
|  .
|
 .
|  .
|
 .
|  .
|
 .
|  .
|
 .
|  .
|
 .
|  .
|
 .
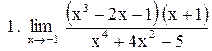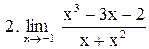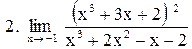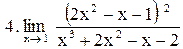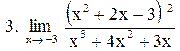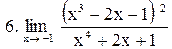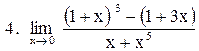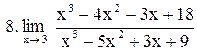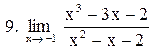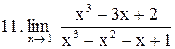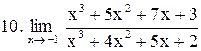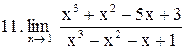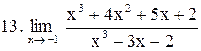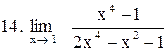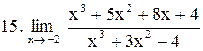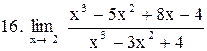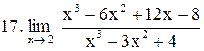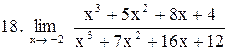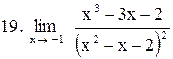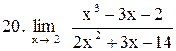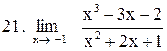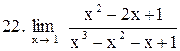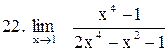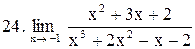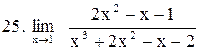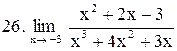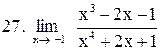| 28.  .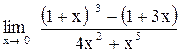
|
 .
|  .
|
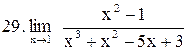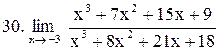З а д а ч а 13
Если в числителе или знаменателе стоят иррациональные выражения, то для получения сомножителя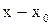 
умножим числитель и знаменатель на сопряженные им выражения.
