Пример 5. Имеются следующие данные о распределении рабочих по затратам времени на обработку одной детали

Имеются следующие данные о распределении рабочих по затратам времени на обработку одной детали:

Затраты времени на одну деталь, мин., х	Число рабочих, чел., f	Сумма накопленных частот,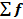
4,5-5,5
5,5-6,5
6,5-7,5
7,5-8,5
8,5-9,5
9,5-10,5
10,5-11,5
ИТОГО:

Определите моду и медиану.

Решение:

В интервальных рядах распределения с равными интервалами мода и медиана определяются по формулам:

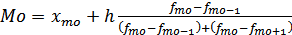
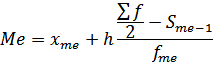
Для нахождения моды находим во второй графе наибольший вес (число рабочих). В нашей задаче это 30 человек, соответственно модальным интервалом будет являться интервал от 7,5-8,5. Теперь по формуле подставляем наши значения:

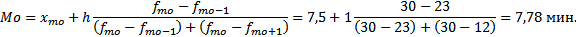
Следовательно, наибольшее количество рабочих затрачивает 7,78 мин на изготовление одной детали.

Для вычисления медианы надо определить сумму накопленных частот ряда, составляющую больше половины общей суммы частот. В графе 3 накопленная сумма частот равна 79. Соответственно, наш медианный интервал будет так же 7,5-8,5.

Подставляем наши данные в формулу:

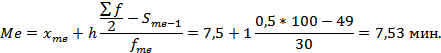
Таким образом, одна половина рабочих затрачивает на обработку детали до 7,53 мин., другая – свыше 7,53 мин.