2015-04-30
460
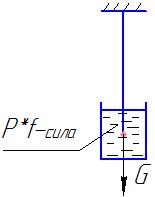
Система весом G помещена в среду с коэффициентом трения «F», т.е. на систему действует сила трения Py’, препятствующая движению.
Под действием мгновеннодействующей силы система получает прогиб «y», необходимо определить максимально возможную деформацию.
; 
; 
; 
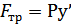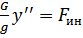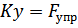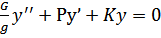(150)* - уравнение равновесия системы;
; 
; 
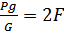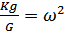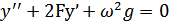(151) – линейное DY без правой части. Его решение ищется в виде одного корня. При н.у. его решение:
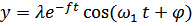(152); 
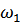- частота собственных колебаний в реальной среде, т.е. учётом коэффициента трения: 
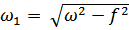(153)
Из (153) видно, что при больших коэффициентах трения, т.е. для вязких сред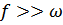 
и подкоренное выражение будет отрицательным, следовательно 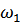будет множественным числом.
Это означает, что колебания будут проходить с амплитудой не переходящей через центр равновесия или центральную осевую линию.
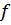- гасящие колебания называются диссипативными силами. Колебания занимающие положения равновесия по одну сторону от осевой называется апериодическими.
Графическое изображение (152) с учётом (153)
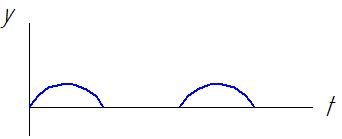
На практике в химической промышленности 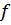=0,1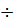 
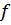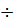0,6 и для стержневых конструкциях =0,02 0,05.
Из (152) видно, что максимально отклонения будут при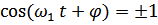 
или 
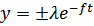(154)
Графическое изображение (154):
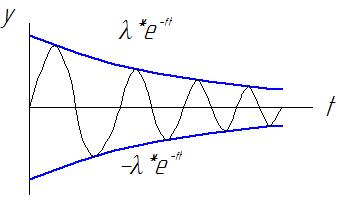
Рассматриваются 2-е амплитуды, отличающиеся по периоду:
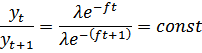
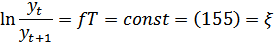
Отношение 2-х амплитуд является величиной постоянной, логарифм их отношения называется логарифмическим декрементом затухания на практике для химической промышленности в аппаратах с мешалкам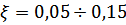и 
при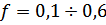 
.
Для стержневых конструкций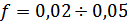 
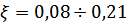. При апериодических колебаниях любая точка системы асимптотически приближается к положению равновесия не переходящая на его другую сторону.
