Собственные колебания

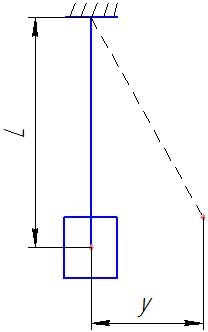
Система закреплена неподвижно на каком-то расстоянии L. Первоначально системе сообщается какой-то импульс (а затем источник сил убирается).

Под действием мгновенно-приложенной силы система отклоняется от положения равновесия на расстояние «y», за счёт сил упругости система стремится занять положение устойчивого равновесия и в какой-то момент времени она его занимает. Т.о. на систему действуют 2-е силы:

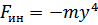(131)** - сила инерции;

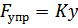(132)** - сила упругости.

Обычно эти силы противоположно направлены и инерционная сила берется со знаком «-». Согласно закону Гука эти силы должны быть равны: 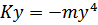или 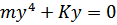(133)^** - линейное дифференцирование уравнение 2 порядка.

Для решения необходимо освободиться от коэффициента при 2-й производной:

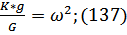
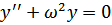(134); K – коэффициент упругости.

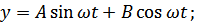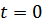
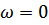
В результате решения (134) путём подбора корней Эйлера получим: при 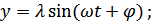( 135)

K – коэффициент упругости зависит от способа закрепления системы.

Наименование	Схема	Формула
Консольная балка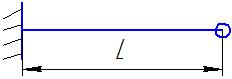
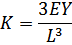
Консольная 2-х опорная балка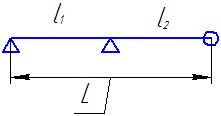
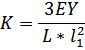
Консольная 2-х пролётная балка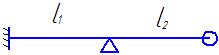
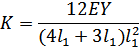
2-х пролётная,2-х опорная балка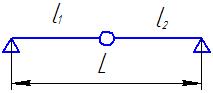

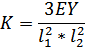
При решение (135) при начальных условиях 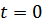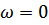получим максимально-возможное отклонение системы от положения равновесия.

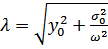(136) на практике (136) пользоваться невозможно, т.к. для великого множества механических систем, использованных в производстве невозможно определить начальные отклонения, поэтому из (137) с учётом коэффициента упругости для данного закрепления:

.

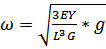Величина «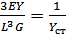» называется статическим прогибом, т.е. прогибом системы при действии частоты собственных колебаний, тогда 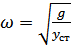; При 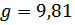см/с²: 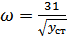; ; 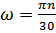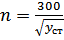(138)

(138) будет характеризовать критическое число оборотов вала для обеспечения минимального статического прогиба.

(138) можно было бы использовать при механических расчётах, если известна величина статического прогибы; в большинстве систем она неизвестна.