Дифференцирование сложной функции.
Пусть 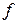 дифференцируема в точке
дифференцируема в точке 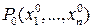 и пусть
и пусть 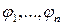 – функции одного переменного, дифференцируемые в точке
– функции одного переменного, дифференцируемые в точке 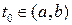 и такие, что
и такие, что 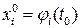 ,
, 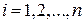 . Тогда сложная функция, составленная из
. Тогда сложная функция, составленная из 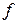 и
и 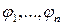 дифференцируема в точке
дифференцируема в точке 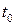 и её производная находится по формуле
и её производная находится по формуле
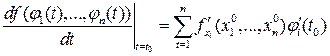 (5.7)
(5.7)
Дифференцирование неявных функций.
Если 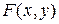 непрерывно дифференцируема в области
непрерывно дифференцируема в области 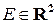 и существует функция
и существует функция 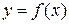 , определенная в
, определенная в 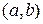 и такая, что для всех
и такая, что для всех 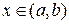 уравнение
уравнение 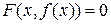 выполняется. А кроме этого
выполняется. А кроме этого 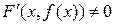 , то
, то 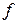 дифференцируема в
дифференцируема в 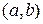 и для каждого
и для каждого 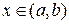 справедливо равенство
справедливо равенство
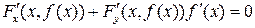 или
или 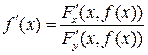 (5.8).
(5.8).
 2015-04-30
2015-04-30 572
572








