2015-04-30
300
Пусть функция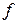 
на множестве
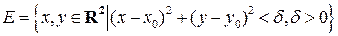
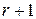раз дифференцируема. Тогда для всех 
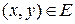справедлива формула
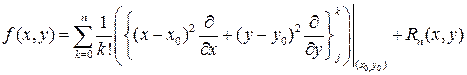(5.9)
При этом
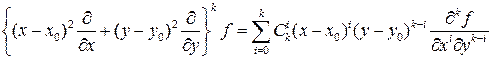
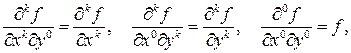
(5.10)
где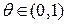 
. Величина 
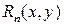называется остаточным членом (в форме Лагранжа) формулы Тейлора для функции .
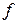Если при 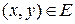имеет место равенство 
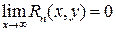, то можно использовать формулу Тейлора для того, чтобы в некоторой окрестности точки 
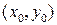приблизить функцию многочленом 
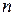-й степени. Формула Тейлора легко может быть обобщена на функции более чем двух переменных.
Если 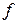дифференцируема в области 
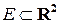и для всех 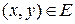выполнены соотношения 
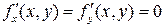, то 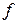- постоянна.
