Если 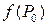 - экстремум функции
- экстремум функции 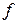 , дифференцируемой по каждой из координатв некоторой окрестности
, дифференцируемой по каждой из координатв некоторой окрестности 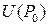 точки
точки  , то выполняются равенства
, то выполняются равенства 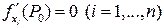 .
.
Достаточные условия существования экстремума.
Пусть функция 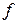 дважды непрерывно дифференцируема в
дважды непрерывно дифференцируема в 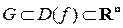 и в точке
и в точке 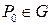 выполняются равенства
выполняются равенства 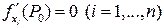 . Если, кроме того, положительно (или отрицательно) определена квадратичная форма
. Если, кроме того, положительно (или отрицательно) определена квадратичная форма
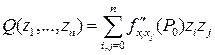 (5.11)
(5.11)
то функция 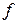 имеет минимум (или максимум) в точке
имеет минимум (или максимум) в точке  , а если форма
, а если форма 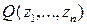 неопределенная, то функция
неопределенная, то функция 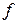 не имеет экстремума в точке
не имеет экстремума в точке  и точка в этом случае называется седловой точкой функции
и точка в этом случае называется седловой точкой функции 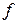 .
.
 2015-04-30
2015-04-30 256
256








