И ИП на их основе 2 страница

Выход из тупика появился при исследовании воздействия магнитного поля на вещество (газы, жидкости, твердые тела). Оказалось, что магнитное поле (внешнее) создает внутри вещества внутренние магнитные поля. С этой точки зрения вещества делятся на три группы:

- Диамагнетики, у которых внутреннее поле направлено встречно внешнему. К ним относятся: газы, вода, цинк, кремний, медь, золото, серебро. Величина внутреннего поля очень мала.

- Парамагнетики, у которых внутреннее поле направлено согласно с направлением внешнего поля. К ним относятся, в частности, алюминий, литий, натрий, калий, титан, вольфрам. Внутреннее магнитное поле парамагнетиков (как и диамагнетиков) очень мало и исчезает при выключении внешнего поля.

- Ферромагнетики, которые подобны парамагнетикам, но создают в десятки тысяч раз более сильные внутренние поля и способны сохранять их при исчезновении внешнего поля. К ним относятся: железо, кобальт, никель, лантаниды, их сплавы.

Практический интерес при разработке ИП представляют, естественно, ферромагнетики, существенно усиливающие собственное магнитное поле контуров с током. Их свойства и характеристики рассмотрим несколько более подробно.

8.2.2. Ферромагнетизм и ферромагнетики

Как мы уже знаем, эксперименты Ампера, Био и других ученых позволили установить, что движущиеся электрические заряды образуют в окружающем пространстве магнитное поле; другие источники магнитных полей не обнаружены. Чем же порождаются магнитные поля у ферромагнетиков, если ток от внешнего источника в них не течет?

Для качественного ответа на вопрос необходимо вернуться к рассмотрению атомной структуры вещества.

Каждый атом вещества состоит из положительного ядра и движущихся вокруг него отрицательно заряженных электронов; причем у электронов имеется два вида движения: вращение вокруг собственной оси (спин) и вращение вокруг положительно заряженного ядра. Следствиями движения электронов должны быть внутренние микроскопические магнитные поля. Так оно и есть у большей части веществ, но разнонаправленность векторов угловых скоростей вращения электронов приводит к взаимной компенсации магнитных микрополей, и внешне их наличие никак не проявляется.

По-другому складываются магнитные условия в ферромагнитных материалах: некомпенсированное магнитное поле электронов внутренних слоев одного атома поворачивает вектора вращения электронов соседних атомов так, что образуются внутренние области однонаправленной магнитной индукции. Области эти, размером порядка сотых долей миллиметра, называются доменами. Соседние домены имеют разное направление магнитной индукции; их разделяют тонкие границы, в пределах которых вектор магнитной индукции поворачивается от состояния одного домена к другому.

Домены и границы можно наблюдать визуально. Для этого образец материала (например, сплав железа) полируют и на поверхность наносят слой порошка окиси железа тонкого помола. Порошок распределяется по границам доменов и их можно наблюдать визуально в микроскоп (см. рис. 8.5).

На рис. 8.5,а, приведена фотография сплава FeSi под микроскопом; на ней ясно видны отдельные домены. Если на образец под микроскопом поместить тонкие отрезки намагниченных проволочек, то их взаимное положение укажет направление индукции поля в каждом домене. Именно этот результат наблюдений представлен на рис. 8.5,б.

Кроме границ доменов, на фотографии образца видны характерные для сплавов неравномерности состава, искажения кристаллических решеток, грязевые и газовые микровключения, называемые дислокациями. В областях дислокаций возникают внутренние механические напряжения, и этим сплавы ферромагнетиков сильно отличаются от кристаллов чистых металлов не только структурой, но и магнитными свойствами.

Что будет происходить с доменами при подаче внешнего магнитного поля, например, если поместить образец ферромагнетика в соленоид с током в обмоткес индукцией исходить с доменами при подаче внешнего магнитного поля? ов неравномерности состава, грязевые и газовые включения н? Для понимания происходящих процессов, будем внешнее поле плавно увеличивать по модулю, сохраняя его направление.

При очень малых внешних полях векторы индукции доменов, близкие по направлению внешнего поля, будут поворачиваться по направлению вектора индукции внешнего поля; границы доменов начнут смещаться, увеличивая размеры отдельных доменов с совпадающими векторами индукции. Общая намагниченность образца ферромагнетика станет отличной от нуля, и индукция суммарного поля будет больше, чем поле соленоида без ферромагнетика.

Для количественного анализа изменений индукции поля, необходимо ввести параметр, количественно характеризующий влияние ферромагнетика. Делается это следующим образом. Вводится характеристика той части магнитного поля, которая не зависит от среды. Она называется вектором напряженности магнитного поля Н; в вакууме (или в воздухе) эта величина отличается от магнитной индукции В только на магнитную постоянную μ ₀:

Н = В / μ ₀. (8.22)

Размерность напряженности магнитного поля – А/м.

В воздухе, следовательно, модуль индукции поля равен его напряженности Н, умноженной на магнитную постоянную μ ₀. А в присутствии ферромагнетика индукция В возрастает во столько раз μ, во сколько ферромагнетик увеличивает начальную напряженность внешнего поля Н:

В = μ₀ μ Н. (8.23)

Величина μ называется магнитной проницаемостью среды; она показывает, во сколько раз увеличилась индукция внешнего магнитного поля при суммарном действии внешнего поля и поля ферромагнетика. Для ферромагнетиков из различных материалов значение магнитной проницаемости (безразмерная величина) лежит в диапазоне от 1·10³ до 1·10⁵.

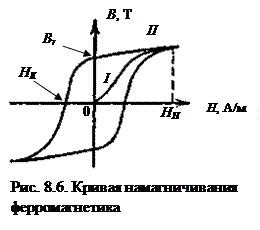Теперь можно зависимость магнитной индукции от напряженности магнитного поля показать графически (рис. 8.6) и продолжить рассмотрение примера, когда ферромагнетик находится в соленоиде. По оси абсцисс отложена величина модуля внешнего намагничивающего поля Н, по оси ординат – значения суммарного (с полем ферромагнетика) поля В, которое больше порождающего в μ раз.

Итак, первое намагничивание ферромагнетика идет по кривой I. Как указывалось выше, на начальном участке намагничивания (в районе, близком к нулю внешнего магнитного поля), увеличение индукции связано с поворотом на небольшой угол векторов индукции доменов, близких по направлению к вектору магнитной напряженности Н.

Дальнейшее увеличение модуля напряженности Н усложняет картину физических процессов намагничивания: по направлению внешнего поля начинают поворачиваться домены с направлениями векторов индукции сильно отличающимися от внешнего. Стенки доменов теперь смещаются скачками: дойдя до неоднородности (дислокации) они останавливаются, не в силах ее преодолеть. Дальнейший рост поля приводит к отрыву стенки домена от дислокации и быстрому ее перемещению в новое положение.

Но быстрое движение намагниченной стенки в металле, по закону электромагнитной индукции, создает электрический ток. Этот ток (называется он током Фуко), движется по замкнутым цепям в объеме металла и его энергия полностью переходит в тепло. Следовательно, процесс намагничивания становится необратимым – при снятии внешнего поля возврат доменов в исходное положение возможен только при компенсации потерь энергии на нагрев образца.

Наконец, при напряженности поля насыщения Н_Н все домены повернуты по вектору напряженности; дальнейшее увеличение напряженности внешнего поля ведет к очень незначительному росту индукции, пропорционально μ ₀ Н. Поэтому линия намагниченности I после Н_Н идет почти параллельно оси абсцисс.

Теперь уберем внешнее поле, на графике рис 8.6 это означает движение от Н_Н к 0. Размагничивание пойдет по кривой II. В точке Н = 0 образец ферромагнетика будет обладать остаточной индукцией В_r, т.е. он становится постоянным магнитом.

Подадим в соленоид ток обратного знака, создавая магнитную напряженность противоположного направления (на рис. 8.6 это движение по оси Н в отрицательную область). Энергия приложенного внешнего поля будет использоваться для компенсации тепловых потерь при намагничивании и поэтому образец продолжит размагничиваться. При напряженности внешнего поля Н_К произойдет полное размагничивание образца и индукция станет В = 0.

Напряженность Н_К называется коэрцитивной силой. Эта сила характеризует ту напряженность внешнего поля, которую необходимо приложить к постоянному магниту, чтобы его размагнитить. Дальнейший процесс перемагничивания образца идет симметрично относительно начала координат.

Площадь внутри замкнутой кривой намагничивания от + Н_Н до – Н_Н и обратно характеризует тепловые потери на перемагничивание образца: чем больше Н_К, тем больше площадь внутри кривой намагничивания и, следовательно, потери энергии внешнего источника поля на перемагничивание образца.

Подводя итоги рассмотрения ферромагнетиков, можно отметить следующее:

- Ферромагнетики в десятки тысяч раз увеличивают магнитное поле катушек с током, являясь, тем самым, основой для создания малогабаритных электрических и электронных устройств, в том числе ИП.

- Вместе с тем, ферромагнетикам присущи три существенных недостатка. Первый - нелинейность зависимости индукции от напряженности внешнего поля, что приводит к нелинейным искажениям сигналов. Второй - большие потери на перемагничивание образцов, вызванные дислокациями, что при переменном внешнем сигнале ведет к потерям энергии источников сигнала и сильному нагреву конструкций устройств. Третий – возникновение токов Фуко (характерных для всех металлов), увеличивающихся с ростом частоты сигнала и ведущим к очень большим тепловым потерям.

Недостатки ферромагнетиков не являются абсолютными: например, постоянный магнит должен иметь большую коэрцитивную силу, чтобы не размагнититься в процессе эксплуатации, а сердечники трансформаторов желательно иметь с предельно малой коэрцитивной силой, чтобы исключить перегрев устройства и снижение коэффициента полезного действия. Поэтому создание ферромагнитных материалов идет несколькими путями.

Для постоянных магнитов создаются сплавы со структурой в виде микроскопических гранул с дислокациями на границах. Подобные сплавы (обычно сплавы сложного состава типа Fe + Cu + Al + Ni + Co) называются магнитотвердыми. Образцы этих сплавов намагничивают в сильных магнитных полях (часто в процессе застывания сплава). Большая коэрцитивная сила подобных сплавов не позволяет им самопроизвольно размагнититься; так получаются образцы постоянных магнитов.

Для трансформаторов, электродвигателей, сердечников индуктивностей разработаны сплавы железа с никелем - пермаллои с малой коэрцитивной силой; они называются магнитомягкими. Для снижения токов Фуко, из магнитомягких материалов прокатывают тонкие пластины, поверхность которых покрывают лаком. Детали (сердечники, магнитопроводы) собирают в виде пакетов указанных тонких пластин.

В высокочастотных приборах, где особенно велики потери от токов Фуко, используются композиции окислов железа с окислами других металлов (ферриты); границы гранул ферритов имеют очень высокое электрическое сопротивление, которое не позволяет развиться большим токам Фуко.

У всех ферромагнетиков с ростом температуры магнитные свойства ослабевают из – за хаотических тепловых колебаний атомов в кристаллах; при определенной температуре (обычно выше 550 – 700⁰С) магнитные свойства ферромагнетиков резко пропадают.

У железа определяющей причиной исчезновения доменов является не температура образца, а изменение кристаллической структуры металла – объемоцентрированная кубическая решетка переходит в гранецентрированную [11]. Оказывается, подобного эффекта можно добиться при низких температурах, если сделать сплав железа с никелем и хромом. При этом получается нержавеющая сталь, сохраняющая прочностные характеристики обычной стали, но прозрачная для магнитных полей. Такую сталь удобно использовать там, где нужно обеспечить проникновение магнитного поля сквозь прочную конструкцию, как, например, сделано в турбинном расходомере (см. раздел 10.3 и рис. 10.5).

8.3. ИП НА ОСНОВЕ ВЗАИМОДЕЙСТВИЯ ВЕЩЕСТВА

И МАГНИТНЫХ ПОЛЕЙ

8.3.1. Индуктивные ИП

Индуктивными называются преобразователи, в которых входной физический параметр изменяет величину индуктивности L или коэффициент взаимной индукции M. Как правило, подобные ИП не первые в цепи измерительных преобразований. У датчиков давления или силы индуктивному ИП предшествует упругая мембрана; у датчиков уровня, расстояния, профиля поверхности – шток с пружиной.

Рассмотрим схему преобразователя, у которого изменяется индуктивность в функции от величины воздушного зазора (рис. 8.7). Первым преобразователем является мембрана, выполненная из магнитомягкой стали, на которую воздействует измеряемая физическая величина Р (давление среды, линейное перемещение, сила). Мембрана смещается, изменяя величину воздушного зазора δ магнитной цепи сердечника с катушкой и мембраной.

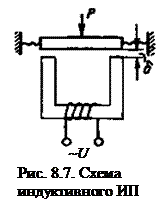Для анализа сопротивления магнитных цепей удобно, как при расчете электрических цепей ввести понятие магнитного напряжения U_M, равного напряженности поля Н, умноженного на длину магнитного пути (для сердечника - это длина средней линии l, для воздушного зазора – его длина δ):

U_M = Н· l.

Но Н, согласно (8.23), равен в ферромагнитной среде индукции поля. деленной на величины магнитной проницаемости Н = В/(μ₀ μ) = Ф/(μ₀ μS), где Ф – магнитный поток через поперечное сечение S участка магнитной цепи.

Следовательно,

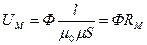, (8.24)

где

R_M = l /(μ₀ μS) (8.25)

называется магнитным сопротивлением участка магнитной цепи. А уравнение (8.24) – законом Ома для магнитной цепи (очевидно, что сопротивление для воздуха будет R_M = l /(μ₀ S)).

Удобство использования закона Ома заключается в возможности суммировать последовательные магнитные сопротивления, а параллельные – рассчитывать как параллельно включенные резисторы.

Для рассматриваемого случая индуктивного ИП магнитное сопротивление магнитопровода R_M складывается из сопротивления в сталисердечника R_MС и сопротивления воздушного зазора R_MВ:

.

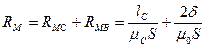Выражение для магнитного потока:

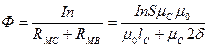, (8.26)

где I – ток в контуре (катушке) преобразователя,

n – число витков катушки,

l_C – длина стальной части магнитопровода.

Индуктивность L, согласно (8.10) равна ψ/I, а ψ = Фn; следовательно

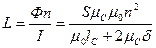. (8.27)

Чтобы индуктивность существенно изменялась при изменении воздушного зазора δ, должно выполняться условие μ₀ ·l_C «μ_C ·δ. При этом выражение (8.27) упрощается

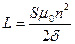. (8.28)

Если под действием измеряемой физической величины происходит приращение воздушного зазора на Δδ, то индуктивность становится равна

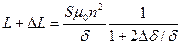. (8.29)

Структура выражения (8.29) точно соответствует случаям параметрических резистивных преобразователей – терморезистору и тензорезистору. Поэтому и оптимальные схемные решения похожи – подача питания от внешнего источника (только переменным сигналом, обычно синусоидальным), выделение изменяемой части параметра (приращения) с помощью мостовой схемы.

Если круговая частота питающего ИП напряжения равна ω, то величина сопротивления индуктивности (пренебрегая омическим сопротивлением катушки) будет пропорциональна величине индуктивности

Z_L = ωL + ωΔL. (8.30)

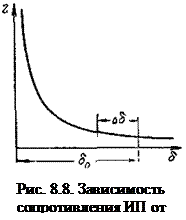Из (8.29) видно, что зависимость между приращением зазора и величиной индуктивного сопротивления носит нелинейный, гиперболический характер; графически он представлен на рис. 8.8.

Как следствие нелинейности функции преобразования, чувствительность преобразователя по диапазону преобразования непостоянна и почти линейный участок зависимости индуктивного сопротивления от приращения зазора Δδ составляет примерно (0,1-0,15)· δ; реально это не более сотых долей миллиметра.

Но для некоторых ИП такие расстояния вполне достаточны. Один случай – преобразование расстояния смещения трубок в кориолисовом расходомере – будет рассмотрен в гл. 10.

Другой случай – преобразователь давления (датчик типа ДД–10) газов, агрессивных и неагрессивных жидкостей представлен на рис. 8.9. Давление Р воздействует на мембрану из магнитомягкого сплава, вызывая ее прогиб. При этом уменьшается зазор между мембраной и сердечником 3, внутри которого намотаны две катушки. Рабочая 1 является частью индуктивного ИП, а катушка 2, включенная последовательно с первой, служит для компенсации влияющих факторов. Соединение с последующими преобразователями происходит через разъем 4.

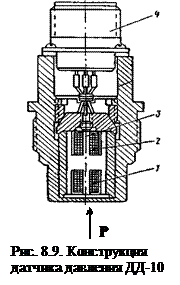Погрешность индуктивного преобразователя определяется несколькими внутренними и внешними факторами: нестабильностью амплитуды и частоты питающего генератора, омическим сопротивлением катушки ИП и емкостным сопротивлением линий связи, нелинейными искажениями, вызванными гистерезисом сердечника. Если компенсационную катушку 2 включить в соседнее с катушкой 1 плечо мостовой схемы, то часть погрешностей, действующих одинаково на обе катушки, будут скомпенсированы (см. ч.1, п. 5.7.2).

Характеристики ИП можно еще улучшить, если индуктивности включены по дифференциальной схеме так, что приращения индуктивностей каждой катушки имеет обратный знак. В этом случае не только снижается воздействие влияющих факторов, но и увеличивается в два раза линейный участок функции преобразования Z(Δδ). Пример подобного ИП уровнемера приведен на рис. 8.10.

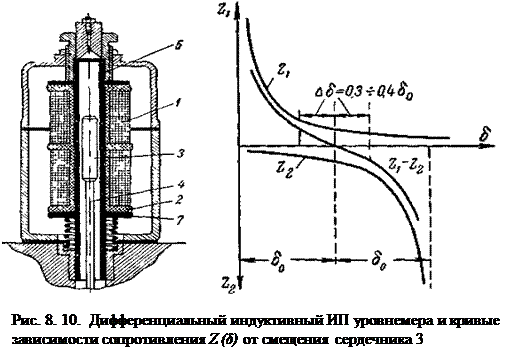
Внутри корпуса ИП на отрезке трубы из немагнитного материала намотаны две одинаковых катушки 1 и 2. Внутри трубы расположен ферромагнитный сердечник 3, перемещаемый немагнитным штоком 4 уровнемера.

При подъеме сердечника 3 относительно среднего положения, растет индуктивность катушки 1 и снижается индуктивность катушки 2; при его опускании – наоборот. На графике представлены кривые изменения сопротивлений индуктивностей катушек Z₁ и Z₂. Там же приведена функция преобразования разности сопротивлений Z₁ – Z₂, соответствующая случаю включения катушек в мостовую схему. Видно, что участок функции преобразования, близкий к линейному закону, увеличился, и крутизна преобразования возросла.

8.3.2. Дифференциальные трансформаторные ИП

Еще лучше компенсируются влияющие факторы и упрощается схема подключения ИП на базе дифференциальных трансформаторов. Идея заключается в том, что питание на чувствительные катушки ИП подается через специальную обмотку, трансформирующую напряжение на обе катушки. Если катушки включить встречно, то отпадает необходимость в мостовой схеме.

Рассмотрим работу подобного ИП на примере оригинальной конструкции измерителя перемещений фирмы Schaevitz [12]. На цилиндре, в котором перемещается сердечник из магнитомягкого сплава, намотаны три обмотки.

Самая нижняя катушка является первичной обмоткой p трансформатора, на которую подают питание. Эта обмотка намотана равномерно, ее плотность (число витков на единицу длины) по длине преобразователя постоянна. Две вторичных обмотки s₁ и s₂ намотаны поверх первичной с плотностью, линейно изменяющейся по длине: у обмотки s₁ плотность нарастает, у s₂ - спадает.

Когда сердечник находится в центре цилиндра, трансформируемые в обмотках s₁ и s₂ напряжения равны по амплитуде и их разность равна нулю. При смещении сердечника в любую сторону разность напряжений будет являться функцией от величины смещения. При такой конструкции ИП почти вся его длина является рабочей, парируются большинство составляющих погрешности преобразования. По данным фирмы - производителя, у указанного преобразователя следующие метрологические характеристики: диапазон линейных перемещений – от 1 до 500 мм; чувствительность – от 1 до 500 мВ на 1 мм перемещений; отклонение от линейности – 0,05 % от диапазона; погрешность от гистерезиса – 0,002% от диапазона измерения.

И последнее замечание: все индуктивные преобразователи имеют большое количество витков провода, поэтому они, с одной стороны, подвержены воздействию внешних магнитных полей, создающих помехи, а, с другой стороны, сами являются источниками магнитных помех. Поэтому индуктивные ИП необходимо размещать в кожухах из магнитомягкого материала с хорошей электрической проводимостью.

8.3.3. ИП на гальваномагнитных эффектах

К гальваномагнитным эффектам относятся явления изменения параметров электрических токов в проводниках при воздействии на них магнитных полей. Мы рассмотрим наиболее часто используемые в ИП эффект Холла и магниторезистивный эффект. Другие эффекты подобного рода можно посмотреть в [25].

Если на проводник с током воздействует внешнее магнитное поле с вектором индукции, перпендикулярной проводнику, то на боковых стенках проводника появляется электрический потенциал. Это явление и называется эффектом Холла. Причиной его является поворот заряженных частиц, движущихся в магнитном поле силой Лоренца согласно уравнению (8.5). В металлах этот эффект крайне мал, а в полупроводниках имеет существенную величину. Поэтому рассмотрим явление на примере пластинки полупроводника n – типа (рис. 8.12).

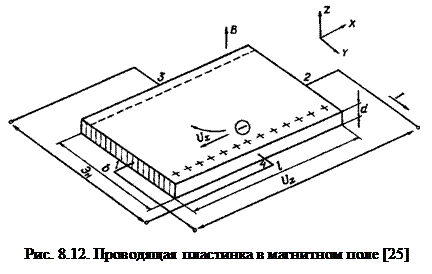
Имеется пластинка полупроводника, через которую от грани 1 к грани 2 под действием напряжения от внешнего источника U_x течет ток I. Если к пластинке приложить внешнее поле индукцией В, то электроны проводимости, создающие ток I, начнут отклоняться, согласно (8.5) силой, действующей по направлению оси Y к краю пластинки 3; соответственно, у края 4 образуется недостаток электронов. А это означает появление между краем 3 и 4 э.д.с. Э_Н, называемый э.д.с. Холла.

В силу ортогональности всех векторов, можно записать в скалярной форме силу, смещающую один электрон к краю 3:

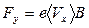, (8.31)

где e – заряд электрона,

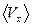- средняя скорость электронов проводимости.

Описанное разделение зарядов приводит к появлению поперечного электрического поля, напряженностью E_y, препятствующего процессу разделения зарядов. В момент равенства противоположно действующих на электрон сил, разделение зарядов прекратится. Приравнивая электрическую силу (силу по закону Кулона) к силе Лоренца получим:

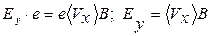. (8.32)

После наступления равенства (8.32) разделение зарядов прекратится и ток в пластинке будет течь как при отсутствии магнитного поля.

Если от одного электрона перейти к плотности тока в пластинке j_х, то напряженность E_y запишется в виде

E_y = - R_H j_xB,

где R_H – константа Холла, зависящая от свойств полупроводника (подвижности зарядов, удельного сопротивления).

Умножим последнее выражение на площадь поперечного сечения пластинки b·d:

E_ybd = -R_H j_xBbd.

Плотность тока, умноженная на площадь поперечного сечения проводника дает величину тока I, а напряженность E_y, умноженная на ширину пластинки b дает значение э.д.с. Холла Э_Н. С учетом сказанного можно записать:

Э_Н = -R_HIB/d. (8.33)

Следовательно, если обеспечить прохождение через элемент Холла (через пластинку) постоянного тока, то э.д.с. на поперечных краях ее будет пропорционален индукции внешнего магнитного поля В. Это же выражение показывает путь повышения чувствительности ИП – необходимо уменьшать толщину пластинки d. Поскольку величину тока повышать нельзя (наступит перегрев пластинки джоулевым теплом), то необходимо уменьшение толщины пластинки сопроводить увеличением ее ширины, сохраняя общую площадь поперечного сечения проводника.

ИП на эффекте Холла используются в измерителях магнитного поля, приборах контроля близости к объектам. Особенно часто они применяются как части преобразователей углов поворота и чисел оборотов различных валов (автомобильных, насосных и т.д.). Для этого в валы запрессовываются постоянные магниты; их поля пересекают при вращении элементы Холла, на выходе которых появляются электрические импульсы.

Теперь рассмотрим магниторезистивный эффект. Он заключается в изменении омического сопротивления проводящей пластинки при воздействии на нее внешнего магнитного поля.

Для достижения такого эффекта достаточно в элементе Холла (рис. 8.12) закоротить между собой края 3 и 4 пластинки. При этом разделенные электроны с края 3 потекут к краю 4 и напряженность E_y, уравновешивавшая силу Лоренца, станет близкой к нулю. Как следствие, разделение зарядов магнитным полем будет происходить постоянно.

При этом большее магнитное поле, создавая большую силу, вынуждает большую часть тока течь не вдоль пластинки, а поперек нее. Внешний эффект получается такой: при постоянном напряжении питания пластинки увеличение магнитного поля приводит к снижению тока во внешней цепи. А отношение напряжения к току есть омическое сопротивление.

К достоинствам магниторезисторов относятся малые размеры и высокая чувствительность: изменение индукции на доли теслы изменяет сопротивление на килоомы. Основной недостаток – зависимость сопротивления от температуры. Недостаток парируется напылением в одной микросхеме четырех магниторезисторов, соединенных в мостовую схему.

Используются подобные ИП, в основном, как преобразователи угла поворота магнитного поля. На их основе создан новый класс электродвигателей – бесконтактные двигатели постоянного тока.

9. ГИДРАВЛИЧЕСКИЕ ПОЛЯ

9.1. ОБЩИЕ ПОЛОЖЕНИЯ

В главе 4, ч.1 было дано краткое описание жидкостей – газовых и капельных. Основное их отличие от твердых веществ – текучесть. Этого оказывается достаточно для возникновения колоссального количества эффектов, не характерных для твердых веществ.

Об одном свойстве жидкостей говорилось в п. 4.1, ч.1 – способности жидкостей принимать форму сосуда, в котором они находятся. Под действием внешних сил жидкости перемещаются. В связи с этим можно говорить о форме движения слоев жидкости – вихревой или поступательной. При поступательном движении подробно исследованы два режима:

- При малых скоростях потока отдельные его части перемещаются не перемешиваясь, слоями. Такой режим называется ламинарным течением.

- При больших скоростях потока отдельные его струйки интенсивно перемешиваются в процессе движения. Такой режим называется турбулентным течением.