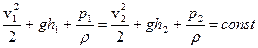И ИП на их основе 4 страница

. (9.15)

Полученное выражение называется уравнением Бернулли, по имени физика, получившего его в 1738 г.

Если участок трубопровода расположен горизонтально h₁ = h₂, или преобразование скоростей и давлений происходит в локальной области, которую можно считать находящейся на одной высоте, то уравнение Бернулли упрощается:

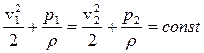. (9.16)

Есть простое измерительное устройство (трубка Пито), позволяющая физически разделить составляющие энергии потока. Трубка Пито представляет собой изогнутую в виде буквы Г трубку, внутрь которой вставлена трубка меньшего диаметра с открытыми концами. У трубки большего диаметра входная часть приварена к трубке меньшего диаметра, а отверстия для поступления жидкости просверлены на боковой поверхности (рис. 9.6). К верхним частям каждой из трубок подключают измерители давления, например, манометры.

Трубка Пито помещается в поток навстречу вектору скорости в исследуемом сечении трубы. Рассмотрим давления, которые будут создаваться в трубках. В трубке большого диаметра отверстия для ввода жидкости никак не изменяют вектор скорости потока, т.е. они не влияют на движение жидкости. Давление, развиваемое в этой трубке равно той части давления, которая не зависит от скорости. В уравнении (9.16) это давление p₁ (или p₂, если трубку установить в другом сечении). Составляющая давления, не зависящая от скорости потока называется статическим давлением p_С.

Определим давление в трубке малого диаметра. Очевидно, что статическое давление p_С, действуя во всех направлениях (по закону Паскаля), создает давление и в трубке малого диаметра. Но, кроме того, набегающая на открытое отверстие струя жидкости полностью останавливается и ее кинетическая энергия ρ ∙v²/2 переходит в потенциальную, т.е. в давление, которое называется динамическим давлением (динамическим напором) p_Д. Следовательно, в трубке малого диаметра создается давление, равное сумме статического и динамического давлений, которое называется полным давлением потока p _П. Согласно уравнению Бернулли энергия потока постоянна, поэтому полная потенциальная энергия остановленного потока равна:

p_П = p_С + p_Д = const.

Теперь можно оценить, как изменяются давления в жидкости при движении в трубе с плавно изменяющимися площадями поперечных сечений (если трубы круглые – то, соответственно, внутреннего диаметра). Например, диаметр трубы уменьшается. По свойству неразрывности потока средняя скорость жидкости нарастает пропорционально квадрату уменьшения диаметра (в порядке напоминания: площадь поперечного сечения пропорциональна квадрату диаметра). При этом растет кинетическая энергия потока. А статическое давление p_С понижается, поскольку суммарная энергия жидкости (или, по-другому, полное давление p_П) остается постоянной величиной; просто изменение диаметра трубы приводит к ее перераспределению между потенциальной и кинетической формами.

9.4.3. Теорема о количестве движения. Гидравлические потери

При рассмотрении законов движения идеальной жидкости неоднократно подчеркивался тот факт, что рассматривается течение при плавных изменениях сечения трубы. Дело в том, что внезапные изменения площади сечения трубы (внезапные расширения или сужения) ведут к необратимым потерям механической энергии. Это означает, что применить закон сохранения механической энергии Бернулли для расчета и анализа потерь не представляется возможным.

Понятно, что потерянная энергия не исчезает, она из механической переходит в тепловую; но механизм и уравнения этого перехода в явной форме не известны. В подобных обстоятельствах полезна теорема о количестве движения; она не описывает детально протекающий процесс, но дает ответ на вопрос о конечном состоянии системы. Теорема, по существу, является следствием второго закона Ньютона: скорость изменения количества движения m v жидкости в выделенном объеме равна сумме сил F, приложенных к выделенному объему с массой жидкости m:

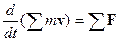. (9.17)

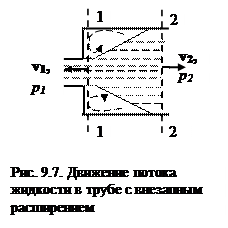Рассмотрим движение жидкости в трубе с внезапным расширением (рис. 9.7). Жидкость течет из трубы с малой площадью поперечного сечения S₁ при средней скорости v₁ и статическом давлении p₁ в трубу большей площади поперечного сечения S₂.

Движение жидкости в трубе большего диаметра имеет сложный характер. В сечении 1-1 струя еще движется компактно, сохраняя площадь сечения S₁, скорость v₁ и статическое давление (по закону Паскаля) равное p₁. При дальнейшем движении струя размывается, занимая все большую площадь, и в сечении 2-2 средняя скорость потока стабилизируется на величине v₂ < v₁ (в силу неразрывности потока), а статическое давление становится равным p₂. Характер и процессы перехода от одной скорости и статического давления к другим не известны. Поэтому для оценки величины p₂ применим теорему о количестве движения.

За время dt струя малого диаметра (в сечении 1-1) переместит жидкость массой ρ·S₁ · dl со скоростью v₁, образуя количество движения ρS₁ dl₁ v₁. По закону неразрывности потока за это же время dt в сечении 2-2 будет перемещена та же масса жидкости, но через другое поперечное сечение S ₂ и с другой скоростью v₂; количество движения жидкости в этом сечении будет равно ρS₂ dl₂ v₂.

Дополнительно необходимо учесть, что скорости, как векторные величины, рассматриваются относительно нормалей к поверхностям, ограничивающим выделенный объем жидкости (на рис. 9.7 это единичный вектор к плоскости 1-1, направленный навстречу вектору скорости v₁ и единичный вектор к плоскости 2-2, совпадающий по направлению с вектором v₂). Поэтому выражение количества движения, вносимого потоком, будет входить в сумму количеств со знаком минус, а выносимых – со знаком плюс:

.

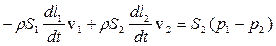В правой части уравнения, согласно выражению (9.17), стоит алгебраическая сумма сил, действующих на выделенный объем; этих сил две: произведение давления p₁ на площадь сечения 1-1, равной S₂, и произведение давления p₂ на площадь сечения 2-2, также равной S₂. Поскольку производная от пути по времени есть скорость, последнее выражение можно записать в следующем виде

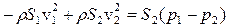. (9.18)

Воспользовавшись уравнением неразрывности потока (9.10), в первом слагаемом (9.18) произведение S₁ v₁ заменим на S₂ v₂ и сократим все выражение на S₂:

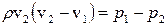. (9.19)

Если бы расширение трубы было плавное и потерь не было, то разность давлений в сечениях 1-1 и 2-2 определялось уравнением Бернулли (9.16)

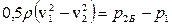, (9. 20)

где p_2Б – статическое давление в сечении 2-2 при отсутствии потерь механической энергии при расширении потока.

Просуммировав почленно выражения (9.19) и (9.20) произведя приведение подобных членов, получим значение потерянной безвозвратно потенциальной энергии Δp

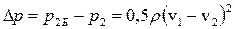. (9.21)

Потеря механической энергии объясняется тем, что на выходе из трубы малого диаметра поток сохраняет высокую скорость и, следовательно, низкое статическое давление в сечении 1-1 трубы большого диаметра. Снижение скорости потока ведет к росту статического давления, которое выдавливает часть потока вдоль стенок трубы в обратном направлении (на рис. 9.7 показано пунктирными стрелками).

Уравнение (9.21) легко преобразовать так, чтобы потери были функцией диаметров трубы в узком и широком сечениях. Для этого вынесем за скобки скорость v₁ и заменим отношение скоростей отношением площадей сечений (по уравнению неразрывности потока)

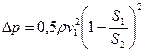. (9.22)

Видно, что при постоянстве площади поперечного сечения трубы (S₁ = S₂) потери давления равны нулю, а с ростом площади S₂ (или уменьшении S₁) потери возрастают и в пределе, при S₂ стремящемся к бесконечности, потери равны всей кинетической энергии потока.

Расчеты, подобные приведенному выше, показывают, что потери давления имеют место и при резком сужении трубы, и при прохождении потока через искривленные участки трубы с малыми радиусами закруглений.. Поскольку потери имеют место даже для модели жидкости без вязкости, тем более следует их ожидать для реальных жидкостей. Эти обстоятельства необходимо учитывать при введении в поток жидкости или газа каких-либо частей измерительных преобразователей

9.5. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ. ВЗАИМОДЕЙСТВИЕ

ГИДРАВЛИЧЕСКИХ ПОЛЕЙ И ВЕЩЕСТВА

9.5.1. Вводные замечания

Рассмотренная в п. 9.4 модель жидкости может быть использована для описания и анализа движения реальной жидкости постоянной температуры, плотности, состава при малых скоростях течения в областях, удаленных от твердых поверхностей. Твердыми могут быть стенки трубы, корпус корабля или элементы ИП, помещенные в поток.

Чем вызвано влияние твердых тел на закон движения жидкости? Тем, что их скорость не совпадает со скоростью движения жидкости или газа: стенки трубы неподвижны, скорости судна или самолета существенно отличаются по направлению и модулю от скорости потока. А реальные жидкости состоят из связанных силами взаимодействия молекул. Те молекулы, что непосредственно касаются молекул твердого тела (например, стенок трубы) прилипают к нему и скорость прилипшего тонкого слоя жидкости равна нулю. За счет сил притяжения тонкий слой неподвижной жидкости препятствуют свободному движению молекул следующего слоя. Возникающие силы называются молекулярными, в отличие от рассмотренных в п. 9.4, называемых массовыми.

При рассмотрении объема жидкости как неразрывного целого, молекулярные силы называются вязкостью и, как было указано в п. 9.2.2, напряжение вязкой силы τ описывается уравнением Ньютона (9.3). Каждая жидкость характеризуется своим динамическим μ или кинематическим ν коэффициентами вязкости, определяемыми экспериментально.

У большинства жидкостей величины коэффициентов вязкости весьма малы и влияют на перестройку скоростей потока в весьма малой области у поверхности твердых тел, называемой пограничным слоем. Однако подобное утверждение не дает представления ни о толщине пограничного слоя, ни о характере скоростей вне и внутри пограничного слоя, ни о характере энергетических процессов в реальных жидкостях. Конечно, на таком уровне знаний понять работу, а тем более разрабатывать ИП, не представляется возможным.

С другой стороны, процессы в реальных жидкостях настолько разнообразны и сложны, что полное изложение всех их особенностей можно найти только в подробных курсах гидродинамики. Мы рассмотрим отдельные, наиболее важные, с точки зрения функционирования ИП, вопросы.

Как указывалось в п. 9.1, общего решения дифференциального уравнения движения вязкой жидкости не существует. А частные решения получаются анализом физических условий течения жидкости и исключением из уравнений слагаемых второго порядка малости.

Поясним сказанное следующим примером [18]. Имеется пористая труба высотой h и диаметром d, через которую течет жидкость. Если высота цилиндра и диаметр одного порядка, т.е. d/h ≈ 1, то торцевые поверхности и боковая поверхность величины одного порядка. Физические эффекты при этом (например, количество жидкости, проходящей через торцевые и боковую поверхность) также одного порядка и они в равной мере должны учитываться при расчете. В случае же, когда d/h «1 (цилиндр бесконечной длины) достаточно рассмотреть задачу определения течения через боковую поверхность. В другом крайнем случае, когда d/h» 1 (труба вырождается в тонкое кольцо) задача сводится к расчету течения через торцевые поверхности.

Таким образом, для величин одной физической природы x и y, которые в конкретных условиях могут принимать значения близкие к x₀ и y₀ критерием порядка будет отношение y₀ / x₀: если отношение близко к единице, например, y₀ / x₀ = 0,5, то величины будут считаться одного порядка. Действительно, число 0,5 никак нельзя считать бесконечно малым второго порядка малости, следовательно, y₀, будучи в два раза меньше параметра x₀, остается с ним одного порядка.

Для дальнейшего анализа осталось определить порядок производных функций, описывающих рассматриваемый процесс. Предположим, что параметр y функционально связан с аргументом x, причем вид функции y = f(x) не известен. Дополнительно известны значения (y₁ и y₂) функции при крайних значениях (x₁ и x₂) аргумента. Для упрощения выражений (без потери общности решения) будем считать, что y₁ = 0 и x₁ = 0. Необходимо определить порядок производной

.

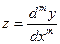Поскольку вид функции y = f(x) и ее производной порядка m не известен, то указать закон изменения функции z не представляется возможным. Но, считая исходную функцию гладкой, можно утверждать, что производная функции изменяется в конечном диапазоне при изменении аргумента x в интервале x₀ = x₂ – x₁ = x₂. Поэтому можно подобрать такое постоянное значение z, которое обеспечит выполнение условия равенства значений исходной функции y = f(x) на концах диапазона изменения аргумента.

Теперь задача формулируется так: найти такую функцию φ(x), значения которой совпадают на концах диапазона с f(x) и m - ная производная которой является постоянным числом. Запишем все условия, которыми определяется искомая функция:

φ(0) = 0; φ(x₂) = y₂; .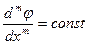

Сформулированным условиям отвечает степенная функция

φ(x) = ax^m, (9.23)

значение которой в конце диапазона равно 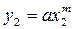; откуда

.

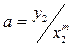Подставив значение a в (9.21) и взяв производную, получим

.

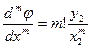Поскольку далее будут рассматриваться производные порядка не выше второго, то факториал не влияет на порядок малости и за меру производной логично принять величину

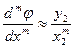. (9.24)

Полученные соотношения порядка позволяют сделать оценочный анализ факторов при движении реальной вязкой жидкости.

9.5.2. Оценка пограничного слоя. Критерий Рейнольдса

Рассмотрим движение невозмущенного потока вязкой жидкости с постоянной скоростью U₀, набегающего на твердую пластину длиной L (рис. 9.8). В слое жидкости, прилегающем к твердой поверхности, за счет сил вязкости, скорость потока u(y) будет изменяться от нуля на твердой поверхности до U₀. Слой, толщиной δ, в котором скорость потока непостоянна, называется пограничным слоем. Выше пограничного слоя вязкость жидкости не сказывается и можно рассматривать течение как течение идеальной жидкости. Какими силами определяется толщина пограничного слоя? Таких силы две:

- сила, определяемая кинетической энергией потока, т.е. массовая сила, обеспечивающая движение жидкости;

- сила вязкости, препятствующая перемещению слоев жидкости относительно неподвижной пластины.

Очевидно, что толщина пограничного слоя характеризуется той областью течения, в которой силы вязкости являются одного порядка с массовыми силами. Установим толщину этой области. Для этого рассмотрим элемент жидкости и определим величины действующих на него сил (рис. 9.9).

Предположим, что жидкость движется параллельно оси x и поступает в выделенный элемент объема со скоростью u. Сила трения на нижней грани выделенного объема равна напряжению трения τ_Н, умноженному на площадь грани dx·dz. А само напряжение трения по грани ABCD, согласно уравнению Ньютона, равно (см. п. 9.2.2)

.

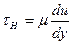На верхней грани MNLE напряжение изменится на величину приращения по оси y, т.е. будет равно

.

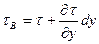Приращение значения касательного напряжения при переходе от нижней грани к верхней будет равно

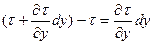
и, следовательно, сила трения на выделенном элементе равна

,

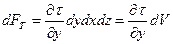где dV = dxdydz – элемент объема.

С учетом выражения для напряжения τ, окончательно формула для силы трения, действующей на выделенный элемент жидкости, приобретает вид

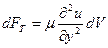. (9.25)

Теперь определим значение массовой силы dF_M, уравновешивающей силу трения в том же элементе жидкости. Для этого достаточно потерю кинетической энергии при прохождении расстояния dx поделить на пройденный путь (см. рис. 9.9):

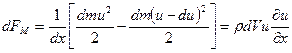. (9.26)

В последнем выражении исключено слагаемое (du)², являющееся величиной второго порядка малости, и учтено, что элемент массы равен плотности жидкости ρ, умноженной на элементарный объем dV.

Поскольку потери силы на перемещение жидкости равно силе трения, то, приравнивая (9.25) и (9.26), получаем равенство

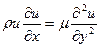. (9.27)

Точное решение дифференциального уравнения заменим оценками, воспользовавшись данными п. 9.5.1. Логично считать, что пограничный слой кончается там, где скорость жидкости u(y) близка к скорости невозмущенного потока, т. е. скорость u имеет порядок U₀.

Длина x по направлению потока имеет порядок длины пластинки L, а в перпендикулярном направлении, по оси y, размер имеет порядок толщины пограничного слоя δ. С учетом соотношения (9.24) получаем вместо точного соотношения (9.27) приближенное равенство

.

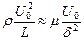В левой части выражения учтено, что порядок u есть U₀, а порядок 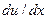есть U₀ / L. Домножив левую и правую часть выражения на L, и выполнив элементарные преобразования, получаем значение толщины пограничного слоя в долях характерного размера (длины пластины L)

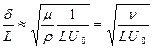, (9.28)

где учтено, что отношение динамической вязкости μ к плотности жидкости ρ есть коэффициент кинематической вязкости ν.

Стоящая в правой части выражения безразмерная величина является обратной важнейшему критерию подобия гидродинамики, а именно, критерию Рейнольдса Re:

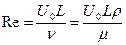. (9.29)

Остановимся на анализе критерия Рейнольдса более детально. В критерий входят скорость, линейный размер и вязкость. Если речь идет о течении жидкостей в трубах, то под скоростью понимают ее максимальное значение (как правило, по оси трубы), а под линейным размером – диаметр трубы.

Критерий выражает соотношение между массовыми силами потока и силами вязкости (трения, сопротивления движению). Если числитель выражения существенно больше знаменателя, то силами вязкости реального потока можно пренебречь при анализе течения жидкости (правда, при этом возникают другие эффекты, которые не упрощают модели движения). И наоборот, если числитель не очень большой (как показали многочисленные эксперименты, при Re ≤ 2000), поток имеет строго упорядоченный характер, описываемый достаточно точными математическими моделями.

Особая ценность критерия Рейнольдса заключается в том, что он является критерием подобия гидродинамических процессов. Это позволяет, исследовав течения жидкости в трубе одного диаметра, распространить полученные результаты (эпюры скоростей, величины гидравлических сопротивлений и т.д.) на трубы других диаметров, другие жидкости и другие скорости при условии сохранения значений критерия.

Конечно, критерием подобия необходимо пользоваться осознанно, понимая эквивалентность используемых моделей. Например, если исследование течения в трубе с водой диаметром 1,5 м заменить исследованием течения в трубе диаметром 0,015 м (увеличив пропорционально скорость течения), то результаты исследований не будут подобны. Дело в том, что для трубы большого диаметра шероховатость ее внутренней поверхности не имеет существенного значения, а для течения жидкости в трубе малого диаметра – это важный неучтенный фактор, и условия подобия процессов не будут соблюдены. Другими словами, модели течений в рассмотренном примере не будут подобны.

Теперь вернемся к выражению (9.28) и запишем его в следующей форме:

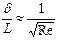. (9.30)

Из последнего выражения видно, что относительная толщина пограничного слоя обратно пропорциональна корню квадратному из критерия Рейнольдса. Следовательно, критерий Рейнольдса выступает как показатель структуры потока. Экспериментами установлено, что при Re ≤ 2000 поток имеет вполне упорядоченную структуру; режим течения при этом называется ламинарным. При значениях Re ≥ 5∙10⁴ течение приобретает устойчивый стационарный характер, называемый турбулентным; его полное теоретическое описание отсутствует, но известны твердо установленные экспериментально основные свойства. Между ламинарным и турбулентным режимами находится переходная зона, в которой скорости отдельных составляющих потока не стационарны, и дать ее теоретическое описание не представляется возможным.

Далее мы несколько подробнее рассмотрим ламинарный и турбулентный режимы течения. Но, с точки зрения измерительных преобразователей, необходимо ясно понимать, что функции преобразования ИП и возникающие погрешности преобразования в определяющей степени зависят от адекватности модели течения жидкости (или газа) реальным процессам в трубопроводах.

9.5.3. Ламинарный режим течения

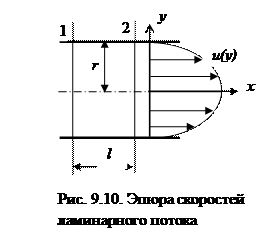
Рассмотрим течение вязкой жидкости в гладкой цилиндрической трубе между сечениями 1 и 2, находящимися на расстоянии l (рис. 9.10). По условию скорость потока такова, что критерий Рейнольдса менее 2000.

Поскольку участок трубы длиной l имеет постоянное сечение, то и скорость потока в нем в установившемся режиме неизменна (по свойству неразрывности потока). В то же время, у реальных жидкостей движению противодействует сила трения (вязкость). За счет чего в таком случае поддерживается постоянство скорости? За счет падения статического давления.

Если обозначить статические давления в соответствующих сечениях через p₁ и p₂, то потеря силы будет определена площадью поперечного сечения πy ², умноженная на падение давления на рассматриваемом интервале (p₁ - p₂). Указанная сила равна силе трения, определяемой как касательное напряжение τ, умноженное на площадь поверхности цилиндра длиной l, т.е. 2 πyl. Получается следующее равенство:

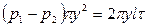, откуда .

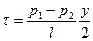В последнем выражении касательное напряжение τ заменим его значением по уравнению Ньютона:

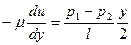. (9.31)

В левой части выражения поставлен знак минус, поскольку при выбранных направлениях координатной системы (координата y нарастает от оси трубы к ее поверхности), приращение скорости имеет отрицательный знак: на оси скорость максимальна, а с ростом y понижается до нуля на поверхности трубы.

Разделяя переменные, получаем интегральное выражение, описывающее изменение скорости потока в поперечном сечении:

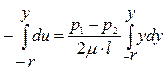
или, с учетом того, что u(-r) = 0 (на стенке трубы скорость равна нулю)

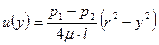. (9.32)

Из (9.32) видно, что при ламинарном течении в трубе круглого сечения распределение скорости имеет форму параболоида вращения (рис. 9.10). На стенке трубы (при y = ± r) скорость равна нулю, а в центре потока (при y = 0) она максимальна и равна

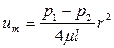. (9.33)

Полученные результаты ясно показывают необходимость уточнения понятия «скорости потока», прежде чем приступать к преобразованию расхода (пусть даже объемного) в другую физическую величину. Действительно, если измерять скорость потока около стенки трубы и умножать результат на площадь поперечного сечения трубы, то расход будет занижен, а если измерять скорость потока по оси, то расход будет завышен.

Для корректного преобразования объемного (или массового) расхода, необходимо, как было указано в п. 9.4.1, предварительно определить среднюю скорость потока. В случае распределения скоростей потока по форме параболоида вращения, средняя скорость определяется из следующих соображений. Как известно из геометрии, объем тела, образованного параболоидом вращения, равен произведению площади основания на половину максимальной высоты, т.е. средняя скорость u_C = u_m /2. Откуда функция преобразования объемного расхода приобретает вид (средняя скорость, умноженная на площадь поперечного сечения трубы):

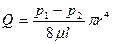. (9.34)

Теперь становится понятно, как можно измерить объемный расход. Во – первых, необходимо изготовить участок трубопровода калиброванного радиуса r и длины l c возможно малыми погрешностями и шероховатостью (такие участки называются мерными). Во – вторых, установить мерный участок в ту область трубопровода, в которой нет поворотов или запирающих устройств. Это обеспечит стабилизацию и симметрию эпюры скорости потока относительно оси мерного участка. Условие весьма существенное, поскольку, как было показано в п. 9.4.3, даже для идеальной жидкости непостоянство сечения трубы, повороты и другие местные нарушения геометрической формы ведут к изменению структуры потока (завихрениям, закрутке и т.д.).