И ИП на их основе 3 страница

Между ламинарным и турбулентным режимами нет резкой границы; область скоростей жидкости, при которой появляются элементы перемешивания отдельных струек, но часть потока сохраняет слоистую структуру, называется переходным режимом. Границы переходного режима весьма условны и сам он не имеет теоретического описания.

Из сказанного становится ясным, что для математического описания движения жидкости необходимо иметь, как минимум, данные о полях сил (обычно рассматривают действие удельных сил, т.е. полей давлений), влияющих на движение жидкости и данные о полях скоростей.

Чтобы модель движения жидкости была хотя бы качественно близка к реальности, необходимо учесть вязкие силы (см. ч.1, п. 4.1) и изменение плотности элементов жидкости при ускорении отдельных ее частей. Действительно, ускорение условно выделенного объема жидкости, обладающего массой, по второму закону Ньютона, создает силу, действующую на соседний объем, что приводит к изменению объема последнего. А при постоянной массе изменение объема как раз и приводит к изменению плотности.

Таким образом, описание поля движения жидкости должно включать в себя векторные поля, характеризующие скорости элементов потока жидкости; аргументами векторов являются три пространственные координаты (в прямоугольной системе координат) и время. Подобные дифференциальные уравнения приводятся в специальной литературе по гидродинамике, но решения для них известны в весьма ограниченном количестве частных случаев.

Для ламинарного потока сжимаемой жидкости при постоянной температуре, отсутствии диффузии (типа, например, растворения спирта в воде) полтора века тому назад было получено дифференциальное уравнение, известное по имени авторов как уравнение Навье – Стокса. До настоящего времени его полное решение не известно. С турбулентным режимом течения до конца не ясна качественная физическая картина процессов, а теоретической ясности еще меньше.

По указанным причинам движение жидкости рассматривают на моделях, из которых исключены факторы, считающиеся несущественными для рассматриваемой задачи. Чаще всего это следующие упрощающие условия:

- постоянство структуры потока и его параметров во времени (стационарное течение);

- отсутствие завихрений (безвихревое течение);

- неизменность плотности жидкости в потоке (условие несжимаемости);

- отсутствие теплопритока, т.е. отсутствие теплообмена, требующего учета при расчетах;

- поле скоростей потока (или вектор средней скорости) направлено по одной оси, например, движение воды в реке или в водопроводной трубе.

Конечно, при анализе реальных процессов движения жидкости редко возникают задачи, в которых можно принять модель движения, включающую все упрощения; но использование даже части из них позволяет решать дифференциальные уравнения до получения расчетных выражений и дает более ясную физическую картину протекающих процессов.

Следуя выработанной в литературе практике изложения, мы последовательно рассмотрим свойства жидкости при нулевой поступательной скорости (гидростатика), законы движения идеальной жидкости, ламинарный и турбулентный режимы течения реальных жидкостей.

Полученные сведения позволят понять принципы работы ИП параметров жидкости и ограничения (или специальные требования по применению), при которых ИП могут реализовать процесс преобразования, не превышая установленных величин погрешности преобразования.

О каких параметрах жидкости или газа, подлежащих измерениям, идет речь? Таких параметров очень много – это вязкость, плотность, давление, температура, поверхностное натяжение и т.д. Но самыми массовыми являются измерения расходов (количества жидкости, проходящих через выделенное сечение в единицу времени) и количества вещества (количество нефти в цистерне, количество кислоты в химическом реакторе и т.д.) Указанная группа составляет 40 % всех параметров, измеряемых в промышленности и науке.

Своеобразие жидкостей не позволяет сейчас, до рассмотрения элементов гидростатики и гидродинамики, указать, что понимать под физическими величинами, определенными выше терминами «скорость», «давление», «расход» и т.д. Это станет ясно по мере рассмотрения физических процессов в жидкости.

9.2. ФИЗИЧЕСКИЕ СВОЙСТВА КАПЕЛЬНЫХ ЖИДКОСТЕЙ И ГАЗОВ

9.2.1. Плотность

Жидкости, не содержащие включений газов или твердой фазы (например, льда) и газы рассматриваются как сплошные среды с переменной в общем случае плотностью ρ(t,x,y,z), определяемой как отношение элемента массы жидкости Δm к занимаемому объему ΔV:

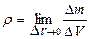. (9.1)

Плотности жидкостей зависят от давления и температуры. Диапазон плотностей примерно такой: жидкий азот при температуре 74 К – 820 кг/м³; вода при 277 К – 1000 кг/м³; ртуть при 310 К – 13000 кг/м³.

Молекулы жидкостей расположены настолько близко и так сильно взаимодействуют при изменении расстояния между ними в процессе сжатия, что при давлениях до сотен атмосфер (десятки МПа) можно считать их несжимаемыми. А изменение температуры (в пределах одного агрегатного состояния, т.е. без перехода в твердое или газообразное состояние) ведет к заметному изменению плотности. Относительное изменение объема жидкости при изменении температуры на 1 К называется изобарным (т.е. определенным при постоянном давлении) коэффициентом расширения β и его значения находятся в диапазоне от 0,1·10^-3 до 2·10^-3. Значит, изменение температуры жидкости, например на 50 К, приведет к изменению ее объема на (0,5 – 10)% и игнорировать эти изменения при измерениях, конечно, нельзя.

Плотность газов в сильной степени зависит от давления и температуры. При давлениях не более 1 МПа можно считать, согласно (4.5, ч.1), плотность пропорциональной давлению и обратно пропорциональной температуре. При более высоких давлениях приходится вводить поправки в уравнение (4.5, ч.1).

Величина поправки, называемая коэффициентом сжимаемости, индивидуальна для каждого газа и приводится в справочниках.

9.2.2. Вязкость

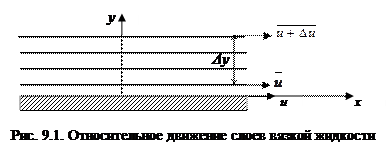
Между слоями жидкости (или газа), текущих с различной скоростью проявляется сопротивление сдвигающим усилиям, некоторое подобие трения между твердыми телами. Например, течение воды в реке. Те молекулы воды, которые касаются дна реки, неподвижны, поскольку связаны молекулярными силами с неподвижным грунтом. Но следующий слой воды (пока не будем уточнять его толщину и характер скорости потока в нем) уже движется.

Молекулы воды, связанные с дном, теми же молекулярными силами связаны с движущимся выше слоем воды и создают касательную (т.е. параллельную скорости движения) тормозящую силу. Эта сила F называется силой вязкости, и величина ее определяется уравнением Ньютона: между параллельными слоями жидкости или газа, движущимися прямолинейно с разной скоростью возникает сила, пропорциональная площади соприкосновения слоев S и градиенту скорости u. При движении жидкости параллельными слоями, градиент скорости равен производной от скорости по нормали y к поверхности слоев (рис. 9.1) и уравнение Ньютона имеет вид:

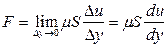. (9.2)

Коэффициент µ, имеющий размерность Паּс, называется динамическим коэффициентом вязкости и определяется для каждой жидкости и газа экспериментально.

При теоретическом анализе течения жидкостей и газов удобно рассматривать величину силы вязкости, приходящуюся на единицу площади контактирующих слоев; величина этой удельной силы называется напряжением вязкой силы τ:

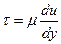(9.3)

В уравнения движения жидкости часто входит плотность ρ как характеристика массовых свойств жидкости. Чтобы уравнения движения из динамических, содержащих плотность жидкости, перевести в кинематические, вместо динамической вязкости µ используют отношение ее к плотности ρ, называемой кинематическим коэффициентом вязкости ν, м²/с:

ν=µ/ρ. (9.4)

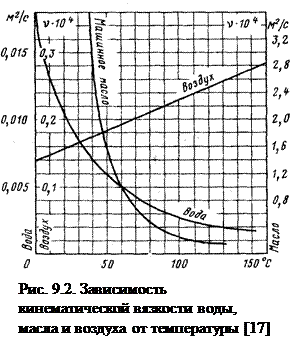Кинематический коэффициент вязкости весьма сильно зависит от температуры (численные данные для широкого класса жидкостей и газов приводятся в справочниках); на рис. 9.2 приведены зависимости от температуры кинематической вязкости воды, масла и воздуха.

Из приведенных кривых видно, что вода является уникальной жидкостью – ее вязкость меньше вязкости воздуха (шкала вязкости воздуха дана правее шкалы воды, а масла - справа от графика).

9.3. ЭЛЕМЕНТЫ ГИДРОСТАТИКИ

В гидростатике изучают законы распределения давлений в покоящейся жидкости и их воздействие на погруженные тела или стенки сосудов.

9.3.1. Закон Паскаля

Рассмотрим элемент малого объема покоящейся жидкости плотностью ρ на глубине h от поверхности. Неподвижность выделенного мысленно элемента означает, что действующие на него силы полностью уравновешены по всем возможным направлениям. Поскольку у капельных жидкостей плотность можно считать постоянной величиной, то давление, оказываемое на элемент жидкости p, определяется давлением газа p₀ на зеркало (поверхность раздела) жидкости и удельной силой земного притяжения столба жидкости высотой h над выделенным элементом (рис. 9.3).

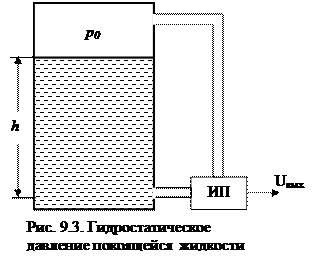Удельная сила Δp, вызванная гравитационным полем Земли, есть давление столба жидкости от зеркала до выбранного элемента, т.е. Δp = ρgh, где g – ускорение свободного падения, а ρh – масса столба жидкости с единичной площадью основания и выстой h. Полное давление на выбранный элемент жидкости равен

p = p₀ + ρgh. (9.5)

Согласно третьему закону Ньютона, выделенный элемент жидкости давит на окружающую жидкость с такой же силой, с какой жидкость действует на элемент. А это означает, в отличие от твердых тел, что давление p действует не только по вертикали, но и по горизонтали (иначе жидкость начала бы течь) и, в частности, создает давление на стенки сосуда. Последнее утверждение составляет содержание закона Паскаля.

Из закона Паскаля следует, что для измерения давления в любом слое жидкости нет необходимости помещать преобразователь давления непосредственно в исследуемый слой. Достаточно вывести трубку на уровне соответствующего слоя и к ней присоединить преобразователь, как это показано на рис. 9.3 (трубка у дна сосуда).

Вернемся к уравнению (9.5). Если измерять давления p и p₀, то можно при известной высоте столба жидкости h получить информацию о ее плотности; функция преобразования будет иметь вид

.

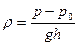Чаще, однако, представляет интерес высота столба жидкости (ее уроваень), которая при известной плотности и измеряемых давлениях имеет уравнение преобразования

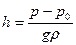. (9.6)

Таким образом, например, удобно определять количество химически активных жидкостей в баках; в этом случае соединительную трубку к ИП давления заполняют нейтральной жидкостью или продувают газом, исключая контакт агрессивной жидкости с мембраной ИП.

При измерении уровня рассматриваемым методом имеется одна тонкость. Рассмотрим ее на следующем примере. Пусть бак на рис. 9.3 является питательным для котельной. В баке находится вода при температуре 100⁰С; для исключения вскипания воды сверху создана паровая подушка с избыточным давлением p₀ = 200 кПа. Максимальная высота столба воды h = 3 м, плотность ее, для простоты вычислений, примем ρ =1000 кг/м³. Преобразование давлений (паровой подушки в верхней части бака и суммарного давления в нижней части бака) в электрический сигнал выполняют серийные датчики давления с относительной погрешностью преобразования γ = 0,5%. Необходимо определить погрешность преобразования высоты столба жидкости в выходной сигнал измерительного устройства.

При полном баке давление, оказываемое водой, на дно бака будет равно

Δp = ρgh = 1000∙ 9,8∙3 ≈ 30000 Па,

а полное давление, преобразуемое датчиком давления, расположенного в нижней части бака, соответственно, 230000 Па.

В выражение (9.6) входят результаты преобразований давлений двумя датчиками давления с относительной погрешностью каждого 0,5%:

- нижнего, измеряющего полное давление p = 230000 Па,

- верхнего, измеряющего давление пара p₀ = 200000 Па.

Если считать, что погрешности каждого из датчиков носят случайный характер, то, как доказывается в курсах метрологии, абсолютная погрешность Δ разности показаний p - p₀ равна абсолютной погрешности одного из них, умноженная на :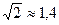

.

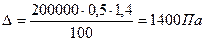Для вычисления относительной погрешности измерения уровня, воспользуемся описанным в п. 2.2.3, ч.1 приемом: прологарифмируем выражение для высоты столба жидкости h = Δp/ρg, определим дифференциалы от левой и правой частей, а потом дифференциалы заменим значениями абсолютных погрешностей:

.

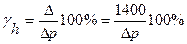Из последнего выражения видно, что даже при уровне воды в баке, близком к максимальному значению 3 м (что соответствует давлению столба жидкости Δp = 30000 Па), относительная погрешность преобразования превышает 4,5%, т.е. в 9 раз больше исходной погрешности использованных преобразователей.

Причина столь большой погрешности заключается в том, что ИП давлений преобразуют всю физическую величину (230 кПа, 200 кПа), а информативной является только часть всей величины (от 200 до 230 кПа).

С подобной ситуацией мы уже встречались при рассмотрении термометров сопротивлений и тензорезисторов. Общий метод преодоления указанной трудности – использование дифференциального (разностного) метода преобразования физической величины. В первом случае это достигалось применением мостовых схем (см. ч.1, п. 5.7.2).

В случае давлений положительный эффект достигается применением вместо двух датчиков давления одного датчика разности давлений. Схематично подобный преобразователь может представлять собой полость, разделенную мембраной; с одной стороны в полость подают жидкость (или газ) с большим давлением, а в другую – с меньшим. В итоге величина прогиба мембраны оказывается функционально связанной с разностью давлений.

Именно такой ИП условно изображен на рис. 9.3. Если даже применить весьма грубый ИП разности давлений с относительной погрешностью 2%, то погрешность преобразования высоты столба жидкости будет в 2 раза меньше, чем в случае применения ИП давлений.

И последнее замечание относительно уравнения (9.6). Необходимо помнить, что мы рассматриваем упрощенные модели физических величин, входящих в уравнение измерения; в частности, плотность жидкости ρ и ускорение свободного падения g приняты постоянными. При измерениях высокой точности необходимо считать плотность жидкости переменной (например, изменяющейся с температурой), а ускорение свободного падения зависящим от географического положения и высоты над поверхностью земли.

9.3.2. Закон Архимеда

Погрузим в жидкость плотностью ρ на глубину h цилиндрическое твердое тело плотностью ρ_Т с площадями оснований S и высотой H (рис. 9.4). Рассмотрим проекцию на вертикальную ось сил, действующих на тело (рассматривать проекции сил на горизонтальную ось не имеет смысла, поскольку твердое тело не создает горизонтальных сил, а гидростатические - уравновешены в соответствии с законом Паскаля).

На верхнюю плоскость тела действует сила, равная ρgSh, равная весу столба жидкости над твердым телом. Само тело создает давление на лежащий под ним слой жидкости с силой веса ρ_Т · gSH. Действие указанных сил направлено вниз. Снизу вверх направлена сила, в соответствии с законом Паскаля, создаваемая слоем жидкости толщиной h + H, и равная ρgS(h + H); эта сила называется выталкивающей.

Теперь необходимо рассмотреть три возможных ситуации.

Первая. ρgSh + ρ_ТgSH > ρgS(h + H). После приведения подобных членов и учета того, что произведение SH равно объему тела V получим ρ_Т · gV > ρgV. Плотность тела ρ_Т выше плотности жидкости ρ, выталкивающая сила меньше веса тела и оно опускается на дно.

Вторая. ρgSh + ρ_Т · gSH = ρgS(h + H). После приведения подобных членов, получим ρ_Т · gV = ρgV. Плотность тела равна плотности жидкости и вес тела равен весу жидкости в том же объеме V (или, по другому, – вес тела равен выталкивающей силе). Тело будет находиться в жидкости в неопределенном состоянии не всплывая и не погружаясь на дно.

Третий. ρgSh + ρ_Т · gSH < ρgS(h + H). В данном случае выталкивающая сила превышает вес тела и оно частично всплывает над поверхностью жидкости. Возникает вопрос: какая часть тела остается погруженной?

Обозначим высоту погружения через H_П. Для погруженной части выполняется, естественно, условие равенства веса тела выталкивающей силе, т.е. ρ_Т · gV = ρgSH_П = ρgV_П, где произведение SH_П =V_П есть объем погруженной части тела.

Рассмотренные три случая объединяются одним утверждением: на тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости в погруженном объеме тела. Это утверждение и является законом Архимеда (древне – греческий ученый, 287-212 г.г. до н.э.).

Применив открытый им закон, Архимед создал один из первых в истории человечества измерительных преобразователей. Измерительная задача формулировалась следующим образом: определить, не добавили ли ремесленники меди в золото при изготовлении короны. Архимед взял золотой слиток весом, равный весу короны, и погрузил по очереди их в сосуд с водой. Поскольку плотность золота выше плотности меди, то при равном весе сплав (золото + медь) занимает объем больше, чем золото того же веса. Поэтому золотой слиток при погружении в воду вызовет ее подъем (за счет вытеснения соответствующего объема воды) меньше, чем при погружении сплава. В современных терминах, Архимед создал ИП, преобразующий физическую величину одного вида (плотность) в величину другого вида (высоту столба жидкости, т.е. в аддитивную физическую величину).

Несколько модифицированные ИП плотности (они называются ареометрами) используются в настоящее время. Это мензурка с помещенным на дне тяжелым телом и делениями на стенке. При погружении в жидкость глубина погружения тем больше (она отсчитывается по количеству делений на уровне зеркала жидкости или датчиком перемещений), чем меньше плотность жидкости.

В заключение вновь подчеркнем упрощенный характер рассмотренной модели. В частности, в рассмотрении не учтено, что воздух также обладает плотностью (а в баках с избыточным давлением – тем более) и создает выталкивающую силу (меньшую, конечно, чем жидкость, но требующую учета при особо точных измерениях).

9.4. ОСНОВЫ ДИНАМИКИ ИДЕАЛЬНОЙ ЖИДКОСТИ

Под идеальной жидкостью понимают жидкость, не обладающую вязкостью, т.е. это модель жидкости, для которой в выражениях (9.2), (9.3) коэффициент вязкости μ = 0. Принятая идеализация означает, что отдельные слои жидкости, перемещаясь в трубе в установившемся режиме, не обмениваются энергией между собой и со стенками трубы. Установившийся (стационарный) режим соответствует случаю постоянства во времени скоростей перемещения жидкости в различных сечениях трубы (хотя они могут быть не равны в различных сечениях).

Поскольку при движении жидкости переносится масса вещества, то возникает вопрос: какие силы вызывают перемещение жидкости? При постоянной температуре таких сил может быть две (или их комбинация):

– сила веса, если труба (или открытый канал) имеет разную высоту над поверхностью земли в различных поперечных сечениях;

- сила, создаваемая насосами (или газом под избыточным давлением); рассматривая силу, приходящуюся на единицу площади поперечного сечения трубы, можно в общем случае считать – жидкость перемещается избыточным давлением.

9.4.1. Уравнение неразрывности потока

Рассмотрим участок трубы, в пределах которого нет источников и потребителей жидкости, т.е. жидкость в трубу не добавляется и не удаляется из нее (рис. 9.5). Площадь поперечного сечения на входе в участок S₁, на выходе из участка – S₂. Количество переносимой жидкости через площадь, например S₁, определяется скоростью жидкости.

Но что понимать под «скоростью», если каждая струйка имеет свой вектор скорости, т.е. индивидуальное направление и модуль.

Условно на рис. 9.5 показаны векторы трех струек в потоке. Под скоростью потока через определенное сечение понимается средняя скорость v, определяемая как средний интеграл от проекций скорости на единичный нормальный вектор n к плоскости сечения S₁. Проекция векторов скорости на единичный вектор n есть скалярное произведение векторов скорости отдельных струек v на вектор n. Окончательно

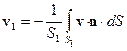. (9.7)

В выражении (9.7) средняя скорость представлена как скаляр, поскольку мы определяли ее модуль по уже выбранному направлению (по оси трубы) и учтено, что вектор скорости и единичный вектор n направлены встречно (отсюда знак минуса перед интегралом). Использованные логические построения позволяют определять среднюю скорость в любом другом сечении, например, в сечении S₂; эту скорость обозначим v₂.

За бесконечно малый интервал времени dt жидкость в сечении S₁ переместится на расстояние dl₁, а в сечении S₂ – соответственно dl₂. Поскольку отсутствуют стоки, то по закону сохранения массы вещества, масса жидкости, втекающей в трубу ρ₁ · S₁ · dl₁ за интервал времени dt, равна вытекающей ρ₂ · S₂ · dl₂. Разделив полученное равенство на интервал времени dt, получим выражение:

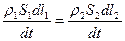, (9.8)

которое необходимо рассмотреть детально.

В числителях дробей стоят произведения элементарных объемов dV = S · dl на плотности жидкости ρ в соответствующих сечениях; а это есть элементарная масса жидкости dm в соответствующем сечении.

Отношение элементарной массы к элементу времени называется массовым расходом Q_m = dm/dt. Массовый расход является физической величиной, наиболее часто определяемой в процессах измерений жидкостей. Объясняется это тем, что в подавляющее большинство уравнений динамики процессов (второй закон Ньютона, кинетические уравнения горения топлив и других химических реакций, перенос тепла, истечение газа из реактивного двигателя и т.д.) входят количества участвующих в процессах молекул или, в макроскопической интерпретации, массы веществ.

Теперь выражение (9.8) можно переписать в виде

Q_m1 = Q_m2. (9.9)

Выражение (9.9) является уравнением (условием) неразрывности потока: при отсутствии источников или стоков жидкости массовый расход в любом сечении трубопровода остается постоянным.

Вернемся к выражению (9.8). Теперь элемент объема S · dl разделим на интервал времени dt. Полученная величина называется объемным расходом жидкости

Q = dV/dt. (9.10)

Объемный расход менее информативен, чем массовый, но его легче измерять; если условия задачи позволяют считать плотность жидкости постоянной, то последующее умножение Q на справочную плотность дает величину массового расхода Q_m. Уравнение неразрывности потока через объемный расход записывается в виде

ρ₁Q₁ = ρ₂Q₂.

Вновь вернемся к выражению (9.8). Теперь на элемент времени dt разделим элемент длины dl, получаем выражение средней линейной скорости потока v в соответствующем сечении трубы v = dl/dt. Уравнение неразрывности записывается через линейную скорость так:

ρ₁ S₁ v₁ = ρ₂ S₂ v₂.

Обычно (особенно для капельных жидкостей) можно считать плотность величиной постоянной. Тогда последнее выражение, определяющее условие неразрывности потока, упрощается и приобретает вид чаще всего применяемый в расчетах

S₁ v₁ = S₂ v₂ = const. (9.11)

Из (9.11) видно, что при уменьшении площади поперечного сечения трубы пропорционально возрастает средняя скорость потока и наоборот, если труба плавно расширяется, то по мере расширения уменьшается скорость течения жидкости в ней.

9.4.2. Уравнение сохранения энергии

При гидравлических расчетах очень часто используется уравнение сохранения механической энергии движущейся жидкостью. Модель жидкости и условия ее движения сохраняются: в трубе с плавно изменяющимися поперечными размерами движется несжимаемая жидкость постоянной плотности ρ с нулевой вязкостью; средняя скорость потока в каждом сечении трубы неизменна во времени (стационарное течение).

Рассмотрим объем жидкости V массой m c геометрической высотой центра тяжести над горизонтальной плоскостью h₁. Жидкость обладает потенциальной и кинетической энергиями.

Кинетическая энергия Э_К1 равна, как известно, 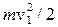, где v₁ – средняя скорость потока в рассматриваемом сечении.

Потенциальная энергия складывается из двух составляющих:

- из энергии положения массы вещества на высоте h₁, это будет mg h₁;

- энергии сжатого давлением p₁ объема V жидкости, это будет p₁V.

Полная энергия Э₁ рассматриваемого объема жидкости равна сумме кинетической и потенциальной энергий

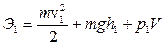. (9.13)

Через некоторое время рассматриваемый объем жидкости переместится по трубе и высота центра тяжести станет h₂, скорость v₂, сжимающее объем давление p₂. Полная энергия того же объема жидкости запишется в виде выражения

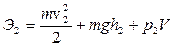. (9.14)

Поскольку, по условию, отсутствуют трение и тепловые потоки, то энергия, по закону ее сохранения, остается постоянной и Э₁ = Э₂, откуда

.

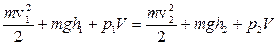В последнем выражении разделим все слагаемые на m = ρ · V: