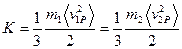И ИП на их основе 7 страница

, (11.5)

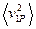где и 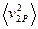- соответственно средние квадраты скоростей газов после достижения равенства температур.

Полная средняя энергия одной частицы одноатомного газа (суммируя поступательную кинетическую энергию по 3 координатам) равна Э₁ = 3 К.

Если вместо одноатомного газа взять двухатомный, например кислород О₂, то у его молекул кроме трех поступательных направлений движения, на каждую из которых приходится средняя кинетическая энергия, равная К, появятся еще три возможных направления, связанных с механической энергией. Во – первых, это колебания каждого атома кислорода по направлению ко второму атому в молекуле: под действием ударов атомы сближаются (кинетическая энергия колебания К) и останавливаются, накопив потенциальную энергию, равную так же К, после чего атомы расходятся, затрачивая накопленную потенциальную энергию. Средняя энергия колебаний одной молекулы равна, следовательно, 2 К. Во–вторых, вращение молекулы вокруг двух осей (молекула не вращается по оси, связывающей два атома); эта энергия так же равна К относительно каждой оси. Полная средняя энергия двухатомной частицы равна Э₂ = 7 К.

В твердых кристаллических телах атомы совершают только колебательные движения в пространстве (по трем координатам) и их средняя кинетическая энергия Э₃ = 6К.

Приведенные данные кинетической теории позволяют сделать четыре важных вывода:

а) Параметром, определяющим состояние термодинамического равновесия вещества и называемым температурой, является средняя энергия его элементарных составляющих (атомов или молекул). Суммарная энергия всего тела (или объема газа, жидкости) носит специальное название – внутренняя энергия.

б) Поскольку средняя кинетическая энергия поступательного движения частиц К кратна другим видам движения частиц, то она может служить мерой внутренней энергии (температурой) при постоянном агрегатном состоянии вещества. Под постоянством агрегатного состояния понимается отсутствие перехода из твердого состояния в жидкое или из жидкого - в газообразное и обратно.

Размерностью такой единицы температуры должна быть размерность энергии (джоуль). Градусы Цельсия, Кельвина и т.д. не отражают физическую суть температуры и ими описывают значения внутренней энергии только в силу исторической традиции.

в) Моделью идеального термометра является находящийся в состоянии термодинамического равновесия с измеряемым веществом баллон с газом низкого давления (близкий аналог идеального газа) и измерителем этого давления.

г) Само понятие температуры может быть применено только к объектам, находящимся в состоянии термодинамического равновесия. Для процессов передачи тепла, когда принципиально отсутствует равновесие, понятие температуры не определено. Возникшую сложность преодолевают, мысленно разбивая физический объект, в котором проводят измерения температуры, на малые локальные области и интервалы времени, в пределах которых можно считать (при заданной погрешности построения модели процесса), что равновесие соблюдается.

Теперь необходимо связать параметры микропроцессов (движения и соударения отдельных атомов или молекул) с параметрами макропроцессов, т.е. процессов такого большого количества вещества, в котором индивидуальные свойства атомов полностью нивелируются и не проявляются. Кроме того, необходимо среднюю кинетическую энергию атомов связать с произвольно выбранной единицей температуры, за которую сейчас принята 1/273,16 часть термодинамической температуры тройной точки воды (тройной точкой называется температура, при которой вода в трех фазовых состояниях – жидкой, твердой и парообразной находится в равновесии; практически эта температура близка к температуре таяния льда). Именно эта единица называется 1 кельвин (или 1 градус Цельсия). Необходимо напомнить, что согласно международному стандарту «Международная температурная шкала 1990 (МТШ – 90)» один градус Цельсия равен одному кельвину по определению.

С точки зрения числа частиц (атомов или молекул) в выделенном объеме V очень удобно рассматривать количество вещества, масса которого равна одному молю. В этом случае для любого вещества количество частиц постоянно – оно равно числу Авогадро N_A = 6,022·10²³ моль^-1. Соответственно, плотность частиц в выражениях (11.1), (11.3), (11.4) для случая одного моля газа запишется в виде

n=N_A / V, (11.6)

а сами выражения приобретут вид

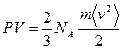. (11.7)

Чтобы в уравнение (11.7) ввести температуру T в принятой шкале, с единицей 1 К или 1⁰ С, необходимо положить, в соответствии с выводом а), что

,

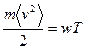где w – коэффициент пропорциональности, который не имеет теоретического смысла; его численное значение может быть определено только экспериментально, исходя из принятого размера единицы температуры.

Выражение (11.7) приобретает вид:

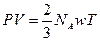. (11.8)

Многочисленные эксперименты позволили установить количественное значение коэффициента связи между произведенной работой в 1 Дж и ростом температуры одного моля газа. Этот коэффициент называется универсальной газовой постоянной R = 2 N_Aw /3 и численно равен

R = 8,3144 Дж/(моль·К).

Подставив в (11.8) значение универсальной газовой постоянной, получим уравнение Клапейрона

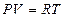. (11.9)

Универсальная газовая постоянная R, отнесенная к одной частице (атому или молекуле) называется постоянной Больцмана k = R / N_A; она характеризует количество энергии, необходимой для повышения температуры частицы на 1 К, и численно равна

k = 1,38·10^-23 Дж/К.

Средняя кинетическая энергия поступательного движения одной частицы, выраженная через температуру, с учетом (11.5), соответственно

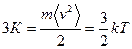, (11.10)

или для отдельно взятой компоненты скорости (например, по оси x)

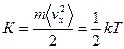. (11.11)

Из сказанного выше легко понять смысл теплоемкости, т.е. количества тепловой энергии, которую необходимо передать одному молю вещества для повышения его температуры на 1 К. Если речь идет об одноатомном газе, частицы которого обладают только поступательным движением, то повышение температуры вызывает рост внутренней энергии (в расчете на один атом) на

Э₁ = 3 К = 3kT /2.

Положив в последнем выражении Т = 1, получим величину приращения внешней энергии ΔЭ₁, которую необходимо затратить для повышения температуры одного атома на один градус:

ΔЭ₁ = 3k /2,

или теплоемкость c_v в расчете на один моль

c_v1 = N_A·ΔЭ₁ = 3R /2. (11.12)

Рассматриваемая теплоемкость c_v является теплоемкостью при постоянном объеме газа. Если при нагреве газу дать возможность расширяться, т.е. увеличивать свой объем при постоянном давлении, то теплоемкость c_р будет больше c_v, поскольку часть тепловой энергии будет расходоваться на совершение работы по расширению газа.

Аналогичные рассуждения приводят к выводу, что теплоемкость моля двухатомного газа c_v2 равна

c_v2 = N_A·ΔЭ₂ = 7R /2,

а кристаллического вещества (закон Дюлонга и Пти)

c_vт = N_A·ΔЭ₃ = 6R /2.

В практических таблицах значения теплоемкостей приводятся не для одного моля, а для единицы массы вещества; размерность ее в этом случае – Дж/(кг·К). Поэтому табличные значения для различных веществ в одном и том же агрегатном состоянии (для газов, твердых веществ) сильно различаются. Вторая причина различий имеет принципиальный характер – рассмотренная выше модель тепловых процессов слишком упрощена; реально же теплоемкости существенно изменяются в широком диапазоне температур, что связано с квантовыми эффектами в веществах. В диапазоне изменения температур технических объектов (от 150 К до 2000 К) значения теплоемкостей приводятся в справочниках; при этом в большинстве случаев в расчетах принимают, что в температурных интервалах 20 – 50 К теплоемкости веществ постоянны.

Тепловые колебания атомов и молекул можно рассматривать как колебания электрических зарядов в диполях, описанных в ч.1, п. 4.5.2. Там показано, что движение с ускорением подобных систем зарядов порождает электромагнитные поля, существующие вне вещества. Другими словами, излученное, например, молекулой кислорода электромагнитное поле может быть поглощено соседней молекулой, увеличив ее энергию, а может излучиться в окружающее пространство.

Поскольку скорости и энергии частиц (атомов или молекул) распределены по закону Максвелла, то и излучения элементарных диполей имеют различные длины волн. Однако основная энергия излучения сосредоточена у волны, излучаемой наибольшим количеством частиц. Длину этой волны, несущей максимум энергии, обозначим λ_m.

Существенным обстоятельством является факт зависимости длины волны излучаемого электромагнитного поля λ_m от температуры вещества Т. Математически эта зависимость описывается законом Вина, согласно которому

λ_m ·Т = b = const. (11.13)

По данным экспериментов константа b = 2,898 ·10^{-3 м ·К.}

Следовательно, чем выше температура, тем меньше длина излучаемой электромагнитной волны. А длина волны λ_m связана с частотой сигнала ν_m следующей зависимостью:

ν_m = с / λ_m, (11.14)

где с – скорость распространения электромагнитной волны; в вакууме это 3 ·10⁸ м/с.

От частоты электромагнитного сигнала зависит количество энергии, которую она переносит, а именно, энергия одного кванта (одного отрезка электромагнитной волны) равна

E = h· ν, (11.15)

где h = 6,626 ·10^-34 Дж·с - константа, называемая постоянной Планка.

Подставив данные из (11.13) и (11.14) в (11.15), получим выражение для количества переносимой электромагнитной волной тепловой энергии на частоте ν_m:

E_m = h ·c ·T / b. (11.16)

Необходимо еще раз подчеркнуть, что речь идет только об электромагнитной волне одной частоты, а не всем совокупном потоке уносимой энергии, который будет рассмотрен в следующем разделе.

Полученные результаты позволяют утверждать, что с ростом температуры вещества растет часть ее внутренней энергии, определяемая электромагнитным взаимодействием элементарных частиц. Чем выше температура вещества, тем выше частота излучаемых электромагнитных волн.

При температурах порядка 1000 К и выше вещество начинает излучать в диапазоне длин волн, воспринимаемых человеческим глазом – оно светится (см. ч.1, таблицу 4.2 в п. 4.5.2). Но с ростом частоты электромагнитных волн растет количество уносимой энергии. Пока в расчете на одну частицу E_m «kT /2 излучением в общем балансе энергии можно пренебречь, что и было сделано выше при изложении кинетической теории.

В заключение рассмотрим вопрос о применении газовых термометров. Действительно, согласно выводу г) большинство вопросов измерения температуры могут быть решены, в принципе, использованием измерительного преобразователя на основе баллона с газом и манометра. Но практически этого не происходит. Для понимания причин крайне редкого применения газового термометра рассмотрим принципиальную схему реального прибора (рис. 11.1).

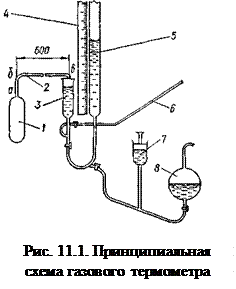Рабочий резервуар 1 заполняется рабочим газом. Капилляр 2 соединяет объем резервуара 1 с коротким коленом манометра 3, частично заполненного ртутью. Колено 3 системой трубок соединено с длинным коленом манометра 5, вытеснительным цилиндром с поршнем 7, вспомогательным резервуаром 8; все трубки и частично емкости заполнены ртутью.

Измерения термометром производят следующим образом. Сначала освобождают манометр от ртути, сливая ее в резервуар 8. По трубке 6 рабочий резервуар 1 заполняется выбранным газом (обычно это гелий при измерениях низких температур или азот). После заполнения резервуара 1 газом трубка 6 отсекается вентилем от остальных магистралей прибора. Далее манометр заполняется ртутью из резервуара 8, который после заполнения отсекается вентилем от манометра. Ртуть в коротком колене 3 поддерживается всегда на постоянном уровне. Контролируют его либо визуально по высоте мениска ртути либо по показанию емкостного ИП. Показания манометра снимаются по шкале 4, которая показывает высоту столба ртути в длинном колене 5.

При изменении температуры давление газа в резервуаре 1 меняется по закону Клапейрона (если считать объем рабочего резервуара, капилляра и короткого колена манометра неизменным); соответственно изменяется уровень ртути в коротком колене. Перемещая поршень в цилиндре 7, добиваются восстановления уровня ртути в коротком колене 3. Уровень ртути в длинном колене 5 изменяется, что фиксируется по шкале 4. Таким образом, температура сначала преобразуется в давление столба ртути, а само давление преобразуется в линейное перемещение. Получается преобразователь с функцией преобразования, в конечном итоге,

L = L₀ + f(T),

где L - высота столба ртути в длинном колене;

L₀ – высота столба ртути при начальной температуре, например, при 0⁰ С;

f(T) – функция, описывающая зависимость приращения высоты столба ртути от температуры.

В принятой модели функция f(T) является линейной. Однако реально изменение температуры изменяет не только давление газа в резервуаре 1, но и его объем из-за линейного расширения стенки резервуара. Кроме того, температура газа в капилляре и коротком колене 3 отличается от температуры в резервуаре 1; температура ртути непостоянна и это изменяет ее плотность; давление газа над поверхностью мениска в длинном колене 5 так же переменно.

Каждый из перечисленных факторов влияния требует тщательного исследования и введения в функцию преобразования соответствующих поправок. Поэтому практически необходимая точность преобразования газовым термометром может быть достигнута только в крупной метрологической лаборатории, где обеспечено выполнение необходимых исследований и условий проведения измерений.

Рассмотренный пример демонстрирует отличие мысленной упрощенной модели ИП от тех реальных проблем, которые возникают при разработке измерительных средств. Упрощенные модели позволяют только понять принцип действия ИП, но не гарантируют полное соответствие действительным свойствам компонентов ИП в реальных условиях применения устройства.

11.3. ЭЛЕМЕНТЫ ТЕОРИИ ТЕПЛОПЕРЕДАЧИ

11.3.1. Общие положения

Из проведенного в п. 11.2 рассмотрения понятия тепловой энергии становится ясным, что состояние «термодинамического равновесия» вещества является идеальной моделью, реализуемой с той или иной степенью приближения. Действительно, если энергия частиц вещества передается при соударении с окружающими частицами, то она неизбежно будет переходить в окружающее пространство, различаться будут только механизмы перехода. Даже если вещество изолировать от непосредственного контакта с окружающими предметами, поместив тело в вакуум (как, например, звезды), то энергия будет теряться за счет электромагнитного излучения.

С другой стороны, допустим, термометр помещен в трубопровод подачи пара на турбину. Согласно кинетической теории, термометр преобразует в электрическое сопротивление (если это терморезистор) или электрическое напряжение (если это термопара) среднюю энергию всех видов движения собственных элементарных частиц. Как эти величины связаны с температурой пара? По–видимому, это зависит от процессов теплопередачи. Не понимая физику процессов невозможно обеспечить близость температуры термометра к температуре измеряемой среды.

Указанные обстоятельства делают необходимым изучение процессов теплопередачи. Как правило, задачи эти крайне сложны, поскольку условий передачи встречается большое разнообразие. Это может быть передача тепла от газа через твердую поверхность другому газу, а может быть от газа только твердой поверхности, или внутри твердой поверхности, в объеме жидкости и т.д. Кроме того, как показали эксперименты, теплопередача зависит от формы тел, скоростей омывающих тела жидкостей или газов, состояния поверхности и даже ее цвета.

Поэтому мы рассмотрим только самые простые модели передачи тепла. Но сначала подчеркнем: как следует из п. 11.2, теплоты, как параметра состояния вещества не существует. Теплота, это, как работа, характеристика процесса. Поэтому создать эталон теплоты и измерять ее количество в веществе, невозможно. Следовательно, говорить можно только о потоке теплоты, или о плотности потока, распространяющегося от более горячих объектов к менее горячим.

Введем следующие определения. Рассмотрим поверхность малой площади S, являющуюся границей тел разной температуры (как в предыдущем пункте стенка между двумя объемами газа). Будем считать температуру поверхности одинаковой по всей площади S. Количество теплоты, переносимой через поверхность S в единицу времени называется тепловым потоком Q.

Поскольку количество тепловой энергии выражается в единицах работы (Дж), то тепловой поток имеет размерность мощности (Вт). Тепловой поток, приходящийся на единицу площади поверхности S, носит название плотности теплового потока q:

q = dQ/dS.

Распространяясь в веществе, тепловой поток создает в каждый момент времени в каждой точке тела свою температуру, а совокупность температур всех точек образует температурное поле Т. Таким образом, температурное поле, в общем случае, есть функция координат x, y, z и времени t:

Т = Т(x, y, z, t). (11.17)

Реальные механизмы теплообмена весьма сложны и их заменяют упрощенными моделями, основанными на трех механизмах теплопередачи:

- теплопроводность - перенос тепла, обусловленный взаимодействием микрочастиц внутри твердого тела или соприкасающихся тел;

- конвекция – перенос тепла вследствие пространственного перемещения вещества; механизм характерен для жидкостей и газов;

- тепловое излучение – перенос тепла посредством электромагнитного поля; состоит, как минимум, из двух превращений – тепловой энергии в электромагнитное поле и наоборот.

Рассмотрим указанные механизмы теплопередачи более подробно применительно к измерительным преобразователям.

11.3.2. Элементы теории теплопроводности

Для упрощения задачи определения закона распределения температур, будем считать, что тепловой поток распространяется только по одному направлению – по оси x, т.е. Т = Т(x, t). Этому случаю соответствует, например, передача тепла из теплой комнаты через стенку на улицу или через корпус термометра к чувствительному элементу. Ось x будем считать направленной перпендикулярно поверхности стенки. Выделим мысленно в стене цилиндр с осью, параллельной оси x и площадью S (рис. 11.2).

Поток тепла dQ, подводимый к сечению x за время dt равен, по определению, плотности теплового потока q(x), умноженного на площадь поперечного сечения цилиндра S и время dt:

dQ(x) = q(x) S dt.

Соответственно, за тот же интервал времени dt через площадь S в сечении x + dx пройдет тепловой поток, равный dQ(x + dx) = q(x + dx)Sdt. Разность величин тепловых потоков на выходе из выделенного объем и на его входе S(x + dx - x) = S·dx равна тому количеству тепловой энергии, которая пошла на повышение температуры рассматриваемого объема стенки S·dx. Это количество тепловой энергии dQ равно

dQ = dQ(x) - dQ(x + dx) =[ q(x) - q(x + dx)] S dt.

Последнее выражение можно записать в более компактном виде, если учесть, что

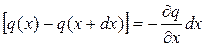
и, следовательно,

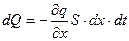. (11.18)

На какую величину повысится температура выделенного объема от действия потока dQ? Для ответа на этот вопрос необходимо учесть, что температура связана с тепловой энергией, переданной телу, параметром, называемым теплоемкость c_v. Поскольку теплоемкость в таблицах дается в расчете на единицу массы вещества, то количество тепла dQ_Т, вызвавшее повышение температуры выделенного объема на dT, равно массе вещества dm выделенного объема S·dx, умноженного на теплоемкость:

dQ_Т = c_v ·ρ · S·dx · dТ, (11.19)

где ρ – плотность материала стенки.

Приравнивая количество выделившегося тепла из (11.18) к количеству тепла, необходимого для повышения температуры выделенного объема на величину dТ, получим выражение, показывающее как меняется приращение температуры выделенного объема стенки от приращения теплового потока:

.

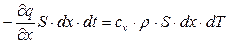Сократив подобные члены, приходим к дифференциальному уравнению

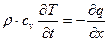. (11.20)

В уравнении (11.20) две неизвестных: скорость изменения температуры во времени и скорость спада плотности потока тепла вдоль пространственной оси x. Для решения уравнения необходимо одну неизвестную выразить через другую. Такую возможность дает закон Фурье, согласно которому плотность потока тепла (в общем случае это вектор q) пропорциональна градиенту температуры:

q = - λ ·grad T.

(В порядке напоминания: градиент есть вектор, величина которого равна производной от скалярного поля Т по пространственным координатам, а направление – по направлению быстрейшего пространственного изменения температуры; подробности см. ч.1, гл. 4). Знак минус показывает, что тепло всегда передается из области высоких температур к низким.

Коэффициент пропорциональности λ характеризует способность вещества проводить теплоту; называется он коэффициентом теплопроводности Размерность его - Вт/(м·К), а численные значения приводятся в справочниках для каждого вещества. В целом можно утверждать, что наименьшей теплопроводностью обладают газы (от 0,005 до 0,5 Вт/(м ·К)), капельные жидкости имеют более высокую теплопроводность (от 0,08 до 0,7 Вт/(м ·К)); наибольшей теплопроводностью обладают твердые вещества (от 0,02 у диэлектриков до 400 Вт/(м ·К) у металлов).

В нашем частном случае, когда тепловые процессы развиваются вдоль одной оси x, выражение для градиента упрощается до частной производной 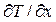, а закон Фурье запишется в виде

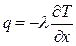. (11.21)

Подставив (11.21) в уравнение (11.20), получим окончательно

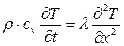. (11.22)

Решения дифференциального уравнения (11.22) для различных частных случаев дают функции распределения температур в пространстве (в веществе) с течением времени. Правда, решение уравнения (11.22) весьма сложная задача и в практических расчетах используют другой прием. Поясним его, решая уравнение (11.22) для случая распределения температуры в поперечном сечении плоской пластинки площадью S и толщиной δ в тот момент времени, когда температурное поле установилось и не меняется во времени (случай стационарного распределения температуры).

В этом случае левая часть уравнения (11.22) равна нулю и остается выражение

.

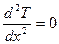Частные производные заменены полными, поскольку, после исключения из числа аргументов времени, осталась одна переменная x. Равенство нулю второй производной означает, что первая производная неизвестного распределения температуры поперек пластинки (по оси x) является постоянным числом и dT / dx = А, где А – неизвестная по величине постоянная интегрирования. Разделяя переменные и интегрируя еще раз, получаем

Т = Ax + B, (11.23)

где В – вторая константа интегрирования.

Для определения постоянных А и В необходимо задаться начальными условиями, т.е. заданными по условию значениями температур на одной стороне пластинки (при x = 0) и на противоположной (при x = δ). Положим, что при x = 0 температура равна Т₁, а при x = δ температура имеет значение Т₂. Подставляя граничные координаты и соответствующие им температуры в выражение (11.23), получаем систему уравнений

Т₁ = В, Т₂ =А· δ + В.

Определив из нее постоянные А и В, найдем распределение температуры в пластинке

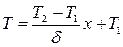. (11.24)

Из последнего выражения видно, что распределение температуры поперек пластинки в стационарном режиме определяется линейным законом (рис. 11.3).

Теперь вычислим тот тепловой поток Q, который обеспечивает постоянное распределение температуры (11.24). Для этого, необходимо плотность потока тепла q умножить на площадь пластинки S, или, с учетом (11.21) и (11.24)

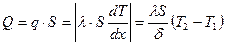. (11.25)

Структура последнего выражения очень похожа на выражение для электрического тока, протекающего через сопротивление. Если считать тепловой поток формально подобным потоку электрических зарядов в единицу времени (ток), а разность температур – подобным разности потенциалов (напряжению), то тепловой поток запишется в виде

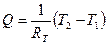, (11.26)

где параметр

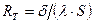(11.27)

обозначается термином тепловое сопротивление стенки.

Решение подобной же задачи для случая цилиндрической стенки (труба, у которой температура вещества внутри, например, пара, отличается от температуры вне трубы), дает следующее выражение теплового сопротивления стенки:

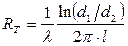, (11.28)

где d₁, d₂ – диаметры соответственно внешней и внутренней стенок цилиндра,

l – длина цилиндра.

Таким образом, решение дифференциального уравнения (11.21) удалось свести к обычному алгебраическому уравнению (11.26). При таком переходе теряется информация о распределении температурного поля внутри вещества, что, как правило, не представляет интереса. Зато резко упростилось решение задач, поскольку тепловые сопротивления можно суммировать как электрические при последовательном и параллельном соединениях.