Как пример, рассчитаем тепловое сопротивление терморезистивного преобразователя температуры в сборе, модель которого представлена на рис. 11.4. Корпус элемента 1 выполнен из стального цилиндра; внутри, между терморезистором 2 и стенкой 1 сделана засыпка из кварцевого песка 3 (для снижения теплового сопротивления); размеры отдельных частей даны на рисунке. Теплопроводность стали (среднее значение) λст = 40 Вт/(м·К), теплопроводность засыпки λз = 0,5 Вт/(м·К).
 Полная тепловая проводимость (величина, обратная тепловому сопротивлению) ИП складывается из проводимости боковой цилиндрической поверхности и проводимости дна стакана (плоского диска). Тепловое сопротивление стального цилиндра, по формуле (11.28)
Полная тепловая проводимость (величина, обратная тепловому сопротивлению) ИП складывается из проводимости боковой цилиндрической поверхности и проводимости дна стакана (плоского диска). Тепловое сопротивление стального цилиндра, по формуле (11.28)
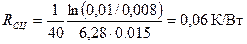 ;
;
сопротивление цилиндрической засыпки, по той же формуле
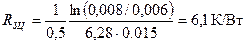 .
.
Общее сопротивление цилиндрической стенки есть сумма последовательных сопротивлений:
RЦ = RСЦ + RЗЦ = 6,16 К/Вт.
Сопротивление стального диска дна стакана определяется по формуле (11.27)
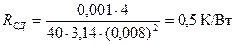 ;
;
по той же формуле сопротивление засыпки дна:
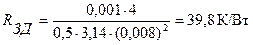 .
.
Общее сопротивление дна стакана RД = RСД + RЗД = 40,3 К/Вт.
Окончательно тепловое сопротивление преобразователя RП равно сумме параллельных сопротивлений цилиндрической стенки RЦ и сопротивления дна стакана RД:
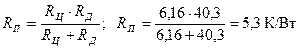 .
.
В практике вычислений и анализа часто удобнее рассматривать не тепловое сопротивление, а тепловую проводимость G = 1/ R (размерность Вт/К); в частности, тепловая проводимость ИП, при известном тепловом сопротивлении RП, равна
GП = 1/ RП.
11.3.3. Пример анализа теплопередачи к ИП
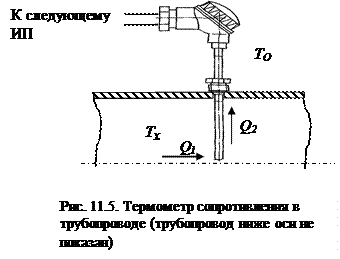
Приведенных выше данных достаточно для рассмотрения упрощенной модели передачи тепла от измеряемой среды измерительному преобразователю температуры, например, термометру сопротивления. Для определенности, будем рассматривать термометр в трубе, по которой течет жидкость с большой теплопроводностью, например, жидкий натрий в теплообменном контуре атомного реактора (рис. 11.5).
Температуру натрия обозначим через Тx, температуру измерительного преобразователя (проволоки терморезистора) через TП температуру внешнего пространства, окружающую трубу и верхнюю часть термометра – через TО. Часть термометра (чувствительный элемент, изображенный на рис. 11.4) погружена в измеряемую среду, а часть – выведена наружу, где к проводам терморезистора подключаются проводники следующих ИП (мостовой схемы, усилителя, блока питания).
 До поступления в трубу горячей жидкости, начальные температуры ИП TПН, трубы и среды в трубе ТХН были равны температуре окружающей среды TО, т.е. ТХН = TПН = TО. В момент времени t = 0 в трубу подается измеряемая среда с постоянной температурой ТХ.
До поступления в трубу горячей жидкости, начальные температуры ИП TПН, трубы и среды в трубе ТХН были равны температуре окружающей среды TО, т.е. ТХН = TПН = TО. В момент времени t = 0 в трубу подается измеряемая среда с постоянной температурой ТХ.
Как бы резко не изменялась температура в трубе, мгновенно прогреть ИП физически невозможно, поскольку для мгновенного нагрева массы датчика (ИП, засыпка, стальной чехол) необходим неограниченный тепловой поток, а он конечен и зависит от величин тепловых сопротивлений элементов конструкции термометра. Поэтому начальные условия имеют вид: при t = 0 температура среды ТХ0 = ТХ; температура терморезистора ТП0 = ТО.
Поступающее через поверхность корпуса термометра тепло со скоростью (тепловой поток) Q, частично идет на нагрев терморезистора (тепловой поток Q1), а частично на теплообмен терморезистора ИП с окружающей внешней средой через засыпку и выходные провода терморезистора (см. рис. 11.4); эту часть потока обозначим через Q2. Уравнение теплового баланса имеет вид
Q = Q1 + Q2. (11.29)
Согласно (11.26) тепловой поток Q1 определяется разностью температур измеряемой среды (константа) ТХ и чувствительного элемента ТП (изменяется во времени)
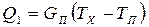 , (11.30)
, (11.30)
где GП – тепловая проводимость преобразователя в сборе; пример его определения дан выше.
Тепловой поток Q2 вычисляется аналогично, только проводимость вдоль засыпки и проводов будет иметь другое значение, обозначим его GК:
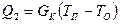 . (11.31)
. (11.31)
Нагрев терморезистора определяется количеством подводимого тепла, его удельной теплоемкостью и массой. Если за время dt подведено тепла Q1·dt, а теплоемкость (произведение удельной теплоемкости на массу) считать равной К, то температура ИП возрастет на величину dTП:
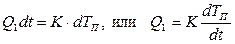 . (11.32)
. (11.32)
Подставляя значения тепловых потоков из (11.30), (11.31), (11.32) в (11.29) получаем выражение теплового баланса через параметры термометра и значения температур:
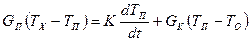 .
.
После элементарных преобразований последнее выражение приводится к виду
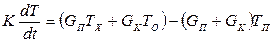 ,
,
в правой части которого в скобки объединены постоянные величины; обозначив их соответственно через А и В, перепишем уравнение в компактном виде:
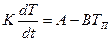 , (11.33)
, (11.33)
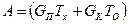 , (11.34)
, (11.34) 

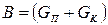 . (11.35)
. (11.35)
Разделяя переменные в дифференциальном уравнении (11.33), получаем выражение
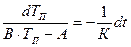 ,
,
интегрирование которого дает в явном виде функцию изменения температуры от времени, параметров среды и преобразователя
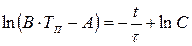 ,
,
или 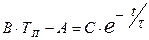 . (11.36)
. (11.36)
В последнем выражении через τ = К / В обозначен параметр, называемый постоянной времени преобразователя, а С – постоянная интегрирования, определяемая начальными условиями задачи. В рассматриваемом случае эти условия сформулированы выше: при t = 0 температура среды ТХ0 = ТХ, температура терморезистора ТП0 = ТО. Подставляя в выражение (11.36) значения А, В из (11.34) и (11.35), t = 0 и значения температур в этот момент, имеем
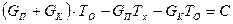 ,
,
откуда
C = (TO – TХ)·GП.
Окончательно зависимость температуры терморезистора от времени и других параметров определяется, если (11.36) решить относительно ТП, с учетом полученных значений констант А, В, С:

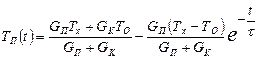 . (11.37)
. (11.37)
График зависимости изменения температуры от времени (в долях τ) представлен на рис. 11.6. Проанализируем функцию изменения температуры и ее график.
11.3.3.1. Во – первых, видно запаздывание прогрева терморезистора (а 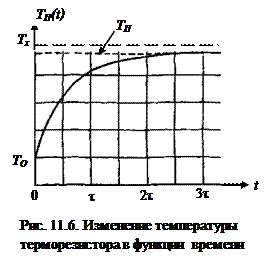 следовательно, выходного сигнала ИП) относительно действительного значения температуры измеряемой среды. Разность значений температуры терморезистора в данный момент времени и температуры измеряемой среды в данный момент времени, есть динамическая составляющая погрешности ИП.
следовательно, выходного сигнала ИП) относительно действительного значения температуры измеряемой среды. Разность значений температуры терморезистора в данный момент времени и температуры измеряемой среды в данный момент времени, есть динамическая составляющая погрешности ИП.
Если температура среды изменяется быстро (например, скачки температуры длительностью 0,1 τ в цилиндре двигателя внутреннего сгорания), то динамическая погрешность окажется абсолютно недопустимой величиной. Величина рассматриваемой погрешности зависит, в основном, от значения постоянной времени τ в показателе степени (11.37): с уменьшением τ второе слагаемое функции будет быстрее стремиться к нулю и оказывать влияние на температуру терморезистора меньшее время.
Поскольку постоянная времени пропорциональна теплоемкости преобразователя K и обратно пропорциональна тепловой проводимости преобразователя (GП + GK), понятны направления конструктивных изменений для ее снижения: необходимо снижать массу проволоки терморезистора, например, заменой ее напыленным в вакууме тонким слоем металла на диэлектрическую подложку; использовать для чехла и засыпки материалы с высокой теплопроводностью.
11.3.3.2. Во – вторых, в статическом режиме, т.е. по прошествии времени более 3 τ температура терморезистора ТП остается ниже температуры среды ТХ. Действительно, положив в (11.37) второе слагаемое равным нулю, получаем значение температуры ТП равным
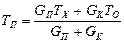 (11.38)
(11.38)
и отличным от ТХ. Величина расхождения есть аддитивная составляющая погрешности ИП Δа, которая равна
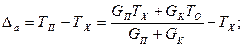
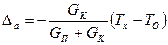 .
.
Из анализа последнего выражения становятся понятны пути снижения аддитивной составляющей погрешности: нужно снизить теплопроводность вдоль преобразователя (если можно, уменьшая толщину защитного цилиндра) и погрузить его в измеряемую среду так, чтобы выполнялось условие GK «GП.
В подавляющем большинстве технических измерений указанных мероприятий оказывается вполне достаточно для реализации условия Δа ≤ 0,1 К.
Второй путь – уменьшение разности температур ТХ – ТО; такое решение, не очень простое в реализации, может оказаться легче, чем разработка преобразователя с более тонкими стенкой и слоем засыпки. Если позволяют условия измерительной задачи (допустимые погрешности, учет температуры холодного спая, уровень помех и другие), то предпочтительней использовать термопару вместо термометра сопротивления.
Весь проведенный анализ выполнен с весьма существенным упрощением, а именно, не был учтен факт подачи в терморезистор электрического тока от внешнего источника. Желательно сделать его величину возможно большей с тем, чтобы увеличить величину падения напряжения на терморезисторе. Как минимум, при этом возрастает соотношение сигнал/помеха, а как максимум – исключается последующий усилитель сигнала (схема измерительного канала упрощается и исчезает один из источников погрешности).
Однако при этом возрастает количество тепловой энергии, выделяемой терморезистором. При электрическом сопротивлении терморезистора RЭ и токе i электрическая мощность, выделяемая как удельная теплота QЭ, определяется законом Джоуля
QЭ = RЭ ·i 2.
Теперь уравнение теплового баланса (11.29) будет иметь вид
Q = Q1 + Q2 + QЭ.
Повторяя проведенный выше расчет с учетом нового слагаемого, в конечном итоге получим выражение для температуры терморезистора ТПi при дополнительном условии протекания через него электрического тока:
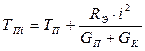 , (11.39)
, (11.39)
где ТП – из (11.38).
Второе слагаемое в (11.39) определяет аддитивную погрешность преобразования 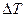 , вызванную протекающим электрическим током
, вызванную протекающим электрическим током
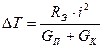 .
.
В правильно спроектированном термометрическом преобразователе, как указывалось выше, выполняется условие GK «GП. Это позволяет упростить последнее выражение и записать его (учтя, что 1/ GП = RП) в виде
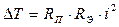 . (11.40)
. (11.40)
При вычислениях по формуле (11.40) необходимо помнить, что RП – тепловое сопротивление, имеющее размерность К/Вт, а RЭ – электрическое сопротивление терморезистора с размерностью Ом.
Используя последнее выражение, можно определить предельно допустимый ток при заданной погрешности от нагрева Джоулевым теплом. Например, необходимо платиновым термометром сопротивления R0 = 100 Ом (т.е. имеющим сопротивление 100 Ом при 00С) и стандартной чувствительностью S = 0,4 Ом/0С измерять температуру горения в топке. Предполагаемая наибольшая температура ТМ = 6000С; предел допустимой погрешности от Джоулева тепла 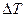 = 0,10С. Для термометров сопротивления в малоподвижном газе тепловое сопротивление RП примерно равно 30 К/Вт.
= 0,10С. Для термометров сопротивления в малоподвижном газе тепловое сопротивление RП примерно равно 30 К/Вт.
Решение. Общее электрическое сопротивление будет равно
RЭ = R0 + S · ТМ = 340 Ом
и допустимый ток iд не должен превышать величины, см. выражение (11.40)
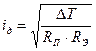 ;
; 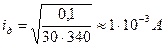 .
.
Относительно значения измеряемой температуры (6000С) требование по погрешности (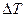 = 0,10С) кажутся необоснованно жесткими. Такое заключение было бы справедливым, если бы речь шла о суммарной погрешности преобразования. Но мы обсуждаем только одну из множества составляющих, поэтому требования по погрешности указанной составляющей не являются чрезмерными.
= 0,10С) кажутся необоснованно жесткими. Такое заключение было бы справедливым, если бы речь шла о суммарной погрешности преобразования. Но мы обсуждаем только одну из множества составляющих, поэтому требования по погрешности указанной составляющей не являются чрезмерными.
11.3.4. ИП на основе конвективного теплообмена
Под конвективным теплообменом, как указывалось ранее, понимается перенос теплоты между выделенной поверхностью и движущейся относительно нее жидкостью или газом. Довольно часто под выделенной поверхностью понимают поверхность твердого тела, но это может быть поверхность раздела, например, жидкости и газа.
В чем отличие механизма конвективного теплообмена от теплопроводности? Отличие заключается в движении макроскопических объемов вещества (жидкости или газа), уносящих в конвективном потоке часть тепловой энергии. Здесь возможны два случая:
- Движение подвижного вещества вызвано внешними побудителями (прокачка жидкости насосом в холодильнике, обдув двигателя вентилятором и т.д.) - режим называется вынужденной конвекцией.
- Движение подвижного вещества вызвано воздействием на него теплового поля – режим свободной конвекции. Например, от батареи водяного отопления нагревается прилегающий слой воздуха. По закону Клапейрона объем его растет при постоянном давлении (атмосферное давление не зависит от работы котельной), а это означает уменьшение плотности воздуха. По закону Архимеда (см. п. 9.3.2) менее плотный газ «всплывает», унося часть тепловой энергии батареи, а на его место устремляется тяжелый холодный воздух.
На процесс конвективного теплообмена, как показали многочисленные эксперименты, влияет множество факторов: скорость потока, форма обтекаемого тела, структура потока и т.д. Описать уравнением все факторы, влияющие на теплообмен, не представляется возможным. Ньютон предложил следующий подход: записать выражение теплового конвективного потока Q (в порядке напоминания: тепловой поток – скорость прохождения тепла от жидкости к стенке или в обратном направлении) в виде
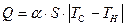 , (11.41)
, (11.41)
где α– параметр, называемый коэффициентом теплоотдачи, размерность м2/с;
S – площадь поверхности стенки, омываемой жидкостью или газом;
ТС – температура стенки;
ТН – температура жидкости или газа вдали от стенки (температура набегающего потока).
Разность температур в выражении (11.41) взята по модулю, чтобы учесть случаи ТС < ТН (например, пар в паропроводе турбины) и ТС > ТН (например, охлаждение полых проводников водой в мощных электрогенераторах).
Поскольку коэффициент теплоотдачи α является комплексным параметром, то его определение в каждом случае представляет большую сложность. С одной стороны, коэффициент является функцией свойств протекающего вещества (теплоемкости, плотности, теплопроводности) и характера его течения (см. раздел 9), а с другой стороны – от характеристик твердой стенки или обтекаемого тела (геометрической формы проходного сечения, наличия ребер и т.д.).
Отсутствие общего аналитического решения уравнений для определения значений тепловых потоков (или разности температур при известном потоке) привели к разработке полуэмпирических методов теории подобия определения коэффициентов теплоотдачи. Методы подобия состоят из двух частей:
- сначала из общих дифференциальных уравнений модели процесса теплопередачи при определенной геометрии поверхности обтекания и структуре потока жидкости (газа) выводится критерий подобия;
- после чего путем многочисленных и тщательных экспериментов устанавливают для каждого обобщенного (подобного) случая соответствующие числовые значения коэффициентов и показателей степени величин, входящих в критерии подобия.
Подробно с указанными методами можно ознакомиться в [18, 21]. Мы рассмотрим только один случай: вынужденный конвективный теплообмен при обтекании твердого цилиндрического тела, например, нагретой электрическим током проволочки малого диаметра, являющейся измерителем скорости потока газа или жидкости.
Итак, предположим, что перпендикулярно вектору скорости газа с температурой ТН установлен цилиндр диаметром d, длиной l (d «l) с температурой стенки ТС. Необходимо определить поток тепла, уносимый движущимся газом с поверхности проволоки.
Предварительно рассмотрим более простую задачу, а именно: тонкую пластинку длиной L, расположенную по координате x, имеющую постоянную температуру ТС омывает с постоянной скоростью U0, направленной параллельно поверхности пластинки, поток газа температурой ТН. Необходимо определить физическую картину теплообмена.
Из анализа гидродинамических процессов известно (см. гл. 9), что тонкий слой газа, контактирующий с поверхностью пластинки неподвижен, следующий слой (в зависимости от вязкости) – движется с незначительной скоростью и т.д. до границы, где скорость потока U0 уже не зависит от наличия пластинки. Относительную толщину указанного переходного (пограничного) слоя вдоль оси y, нормальной к поверхности пластинки, характеризует критерий Рейнольдса Re (см. п. 9.5.2).
Но если у поверхности пластинки газ неподвижен, то теплота в нем передается только за счет теплопроводности согласно уравнению Фурье (см. п. 11.3.2). Следовательно, конвективный теплообмен состоит из двух процессов: передачи тепла непосредственно от молекулы к молекуле как в твердом теле (теплопроводность) и унос тепла движущимся потоком. Причем тепловые процессы происходят в тепловом пограничном слое газа толщиной δТ, прилегающем к поверхности пластинки, в пределах которого температура газа изменяется от ТС до температуры невозмущенного набегающего потока ТН. Остальной газ (вне пределов пограничного слоя) никакого влияния на теплообмен не оказывает. Для оценки эффективности теплопередачи, следовательно, необходимо определить порядок толщины теплового пограничного слоя δТ.
С этой целью вновь рассмотрим уравнение (11.22), которое является уравнением баланса тепловой энергии: сколько приобретает внутренней энергии элемент газа с теплоемкостью cv (и уносит ее за счет движения газа), столько же его отдает первый (неподвижный слой газа) за счет теплопроводности в направлении, перпендикулярном пластинке, т.е. по оси y:
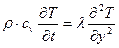 . (11.42)
. (11.42)
Для исключения из последнего уравнения времени, левую его часть умножим и разделим на 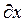 :
:
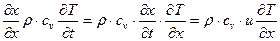 ,
,
где 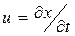 - скорость в пограничном слое.
- скорость в пограничном слое.
Теперь (11.42) запишется в виде:
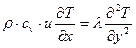 . (11.43)
. (11.43)
Оценим порядок входящих в последнее выражение величин, как это объяснялось в п. 9.5.1 и было использовано в п. 9.5.2. Характерными размерами в данном случае будут: скорость невозмущенного потока газа – U0; расстояние по оси x – длина пластинки L; расстояние по оси y – толщина теплового пограничного слоя δТ; диапазон температур – разность (ТС – ТН). Подставим характерные размеры в (11.43), заменяя ими переменные и их дифференциалы:
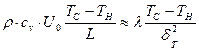 ,
,
откуда после элементарных преобразований
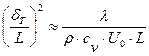 .
.
Отношение теплопроводности вещества λ к его теплоемкости ρ·cv называется коэффициентом температуропроводности а. Перепишем последнее выражение в более сжатом виде:
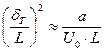 ,
,
или
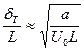 .
.
Последнее выражение по структуре точно совпадает с выражением для относительной толщины динамического слоя (9.26). Безразмерная величина под корнем квадратным, характеризующим толщину теплового пограничного слоя носит название критерия Пекле Pe:
Pe = U0 L / a, (11.44)
и относительная толщина теплового пограничного слоя имеет порядок величины
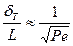 . (11.45)
. (11.45)
Теперь осталось понять, как соотносятся толщины динамического δ и теплового δТ пограничных слоев. Для ответа на этот вопрос достаточно выражение (9.28) разделить на (11.44):
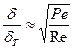 .
.
Отношение критерия Пекле к критерию Рейнольдса показывает насколько пограничные слои и структуры распределения скоростей потока и распределения температур подобны. Это отношение называется критерием Прандтля
Pr = Pe / Re = ν / а,
где ν – коэффициент кинематической вязкости,
а – коэффициент температуропроводности.
Именно критерий Прандтля входит в эмпирические выражения конвективного теплообмена. Экспериментально установлено, что при скоростях газа много меньше скорости звука критерий Прандтля близок к единице (динамический и тепловой пограничные слои имеют одинаковую толщину), а для капельных жидкостей он существенно больше единицы и имеет индивидуальные значения для различных жидкостей.
После проведенного рассмотрения теплообмена газа (жидкости) с пластинкой, можно вернуться к основной задаче определения конвективного теплообмена при обтекании жидкостью или газом цилиндра. Основным уравнением для анализа, как указывалось выше, является уравнение (11.41) связи теплового потока и разности температур стенки и набегающего потока газа (или капельной жидкости). Проблема свелась к определению коэффициента теплоотдачи α.
На основании теории подобия и результатов экспериментов для случая обтекания цилиндра жидкостью выражение для коэффициента теплоотдачи 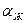 имеет вид [2]:
имеет вид [2]:
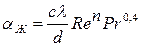 , (11.46)
, (11.46)
где с и n – экспериментально определяемые константы. Для воды, например, эти константы имеют следующие значения (табл. 11.1)
Таблица 11.1
| Re | c | n |
| 5 – 80 | 0.93 | 0.4 |
| 80 - 5·103 | 0.715 | 0.46 |
| > 5·103 | 0.226 | 0.6 |
Данные для вычисления критерия Прандтля (жидкость - вода) приведены ниже
| Температура t, 0С | Кинематическая вязкость ν, м2/с | Теплопроводность λ, Вт/(м·К) | Коэффициент температуропроводности а, м2/с |
| 1·10-6 | 0,60 | 1,4·10-7 | |
| 0,5·10-6 | 0,66 | 1,6·10-7 | |
| 0,4·10-6 | 0,69 | 1,65·10-7 |
Для газов критерий Прандтля близок к единице и выражение (11.46) упрощается до вида
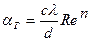 . (11.47)
. (11.47)
Коэффициенты c и n сохраняют значения, указанные в таб. 11.1; изменяются только данные по теплопроводности (например, при температуре 00С воздух имеет теплопроводность 0,024 Вт/(м·К), а водород – 0,17 Вт/(м·К)) и вязкости газов (кинематическая вязкость воздуха 13,7 ·10-6 м2/с, а водорода – 98,0·10-6 м2/с).
Как можно использовать результаты анализа конвективного теплообмена для разработки ИП? Из уравнений (11.41) и (11.47) видно, что если поместить в поток газа (или жидкости) проволочку малого диаметра с температурой ТС, отличной от температуры омывающего газа ТН, то количество уносимого за счет конвекции тепла будет функцией теплопроводности λ и скорости потока U0 (входит в выражение критерия Рейнольдса Re).
Нагреть проволочку можно, пропуская через нее электрический ток. Если сопротивление проволочки R то при токе I выделяемое количество тепла в единицу времени равно рассеиваемой мощности, т.е. I2·R. Пример подобного измерителя скорости, называемый термоанемометром, приведен на рис. 11.7,а. Нить ИП из платины или вольфрама диаметром несколько микрометров и длиной от 1 до 5 мм крепится в вилке 2 из металлических упругих проволок. Проволоки 2 проходят сквозь диэлектрическое тело зонда 3 и кончаются отрезками проводов 4 для подключения источника питания нити и вторичных преобразователей.
 2015-04-30
2015-04-30 356
356








