Скорость и ускорение точки

В естественной системе координат

Определим орт 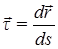, он направлен по касательной к траекто­рии. Вектор 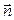ортогонален к орту .

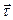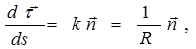
Составим отношение:

где k − кривизна траектории, R − радиус кривизны траектории.

Третий орт 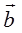определим как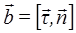

Определим скорость и ускорение точки в естественной системе координат:

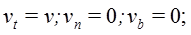
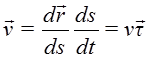
; то есть

Таким образом, скорость точки всегда направлена по касательной к траектории.

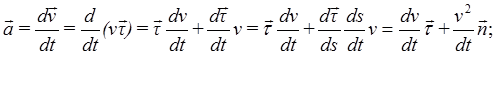
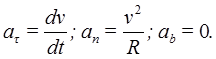
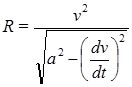то есть

Из последних соотношений получим формулу: