Вычисление определенного интеграла

7.1. Интеграл с переменным верхним пределом

Пусть задана функция, интегрируемая на отрезке . Тогда по свойству 1 определенного интеграла для любой точки 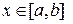функция также будет интегрируема на отрезке 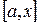. Поэтому определена функция 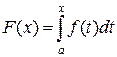, она называется интегралом с переменным верхним пределом.

Теорема 1. Пусть функция интегрируема на отрезке . Тогда функция 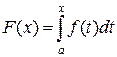будет непрерывной на отрезке .

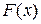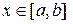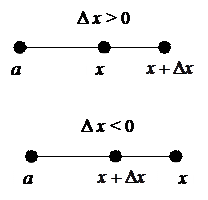
Доказательство. Докажем, что непрерывна в любой точке . Для этого покажем, что приращение 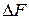функции стремится к нулю, если приращение 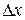аргумента стремится к нулю.

.

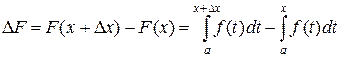Если 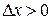, то

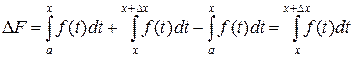
Если же 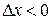, то

.

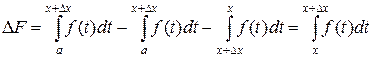Таким образом, при любом приращении переменной приращение функции выражается формулой

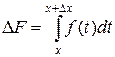. По теореме о среднем 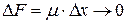при ,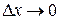

что и требовалось доказать.

Теорема 2. Пусть функция непрерывна на отрезке . Тогда функция 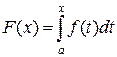будет дифференцируема на интервале 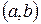, причём выполняется равенство .

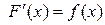То есть интеграл с переменным верхним пределом является первообразной для подынтегральной функции, в случае, если она непрерывна.

Доказательство. Зафиксируем точку 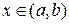. Покажем, что в этой точке существует конечная производная.

.

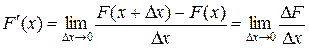Также как в предыдущей теореме выводится формула для приращения функции .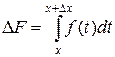

Отсюда по теореме о среднем в случае непрерывной функции получаем

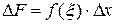, где точка 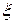является промежуточной между 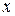и .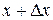

Подставляя выражение для приращения функции в ее производную, получаем .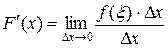

Так как при 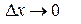точка 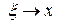, а функция непрерывна в точке ,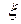

то 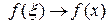и тогда справедлива формула 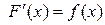, что и требовалось доказать.