Пусть задан отрезок  и функция
и функция  , такая что для всякого достаточно малого
, такая что для всякого достаточно малого 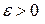 функция
функция  интегрируема по Риману на отрезке
интегрируема по Риману на отрезке 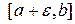 ;
;
кроме того 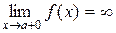 . Тогда несобственный интеграл второго рода определяется по формуле
. Тогда несобственный интеграл второго рода определяется по формуле

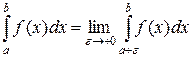 .
.
Если предел существует и конечен, то говорят, что несобственный интеграл сходится. Если же предел бесконечный либо вообще не существует, то говорят, что интеграл расходится.
К несобственным интегралам применимы методы замены переменной и интегрирования по частям.
Пример 3. Исследовать на сходимость интеграл 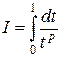 .
.
Если 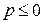 , то подынтегральная функция ограниченна, интеграл является собственным и принимает конечное значение.
, то подынтегральная функция ограниченна, интеграл является собственным и принимает конечное значение.
При 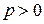 подынтегральная функция
подынтегральная функция 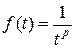 имеет особенность в точке
имеет особенность в точке 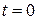 , она обращается в бесконечность в этой точке
, она обращается в бесконечность в этой точке 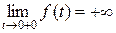 . Значит, это несобственный интеграл второго рода.
. Значит, это несобственный интеграл второго рода.
Сделаем в нем замену переменной 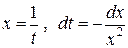 .
.
Пересчитаем пределы интегрирования. При 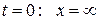 ; при
; при 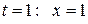 .
.
Подставляя эти выражения в первоначальный интеграл, получаем
 . Этотнесобственный интеграл первого рода исследован на сходимость в примере 1. Он сходится при
. Этотнесобственный интеграл первого рода исследован на сходимость в примере 1. Он сходится при 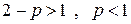 ;
;
расходится при 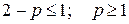 .
.
Итак, интеграл 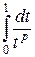 сходится при
сходится при 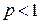 и расходится при
и расходится при 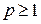 .
.
Этот интеграл также имеет большое значение для исследования на сходимость других несобственных интегралов.
Приложения определённого интеграла
Общая схема приложений определённого интеграла
Пусть задана некоторая величина 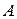 (физическая или геометрическая). Нужно найти её значение на отрезке
(физическая или геометрическая). Нужно найти её значение на отрезке 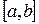 . Пусть величина
. Пусть величина 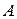 является непрерывной и аддитивной по множеству, то есть из того, что
является непрерывной и аддитивной по множеству, то есть из того, что 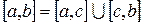 следует, что
следует, что 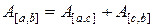 .
.
1) Разбиваем отрезок  на n частей
на n частей 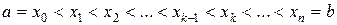 .
.
2) Пусть удается подобрать такую непрерывную функцию  , что значение величины A накаждом частичном отрезке разбиения представимо в виде
, что значение величины A накаждом частичном отрезке разбиения представимо в виде 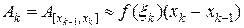 , где
, где 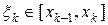 .
.
3) Тогда, в силу аддитивности величины 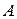 , верно приближенное равенство
, верно приближенное равенство 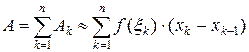 .
.
Сумма, стоящая в правой части этого равенства, является интегральной суммой Римана для функции  .
.
4) Если мелкость разбиения 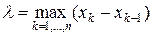 устремить к нулю, то интегральные суммы Римана стремятся к интегралу от функции
устремить к нулю, то интегральные суммы Римана стремятся к интегралу от функции  и приближенное равенство становится точным
и приближенное равенство становится точным 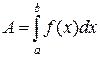 .
.
Более краткое изложение этой схемы.
Приращение величины 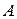 представляем в виде
представляем в виде 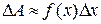 ;
;
отсюда дифференциал величины 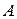 равен
равен 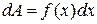 ;
;
затем находим 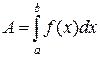 .
.
 2015-05-05
2015-05-05 2539
2539
