2015-05-05
1564
1) Если функция интегрируема на отрезке 
, то она интегрируема на любом отрезке, лежащем в отрезке .
2) (аддитивность интеграла по множеству)
Если функция интегрируема на отрезках и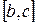 
то она интегрируема и на отрезке 
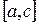. При этом выполняется равенство
.
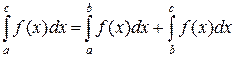3) Если функция 
интегрируема на отрезке и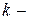 
произвольная константа, то функция 
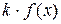также интегрируема на отрезке . При этом выполняется равенство
.
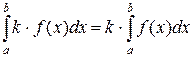Это свойство обычно формулируют так: постоянный множитель можно выносить за знак определённого интеграла.
4) (аддитивность интеграла по функции) Если функции и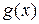 
интегрируемы на отрезке , то их сумма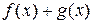 
также интегрируема на отрезке и при этом выполняется равенство
.
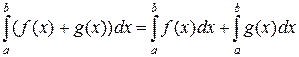5) Интеграл от функции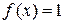 
по отрезку равен длине отрезка
.
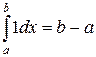6) При изменении порядка пределов интегрирования меняется знак определенного интеграла
.
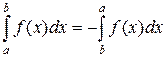7) Если функция интегрируема на отрезке , то её модуль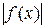 
также интегрируем на отрезке и модуль интеграла не превосходит интеграла от модуля
.
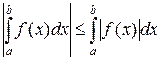8) Если функция интегрируема на отрезке и неотрицательна, то ее интеграл также неотрицателен
|
|
|
.
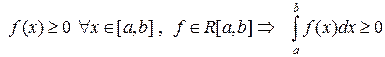9) Если функции и 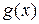интегрируемы на отрезке и функция не превосходит функцию 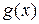, то можно переходить к интегралу в неравенстве
.
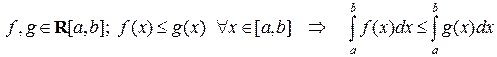10)(оценка интеграла)
.
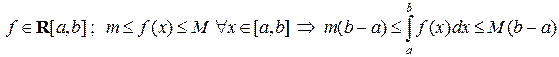11) Теорема о среднем.
Пусть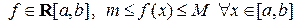 
. Тогда 
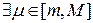, такое что 
.
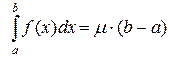В случае если непрерывна на отрезке , найдется точка
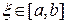, такая что 
.
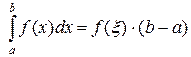12) Обобщённая теорема о среднем.
Пусть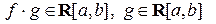 
; кроме того 
.
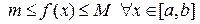Тогда существует число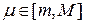 
такое что
.
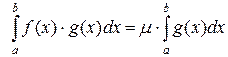В случае если непрерывна на отрезке , найдется точка
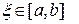такая что
.
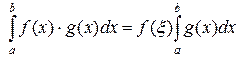Пример. При расчёте нагрузки, на определённый узел конструкции получили следующий интеграл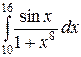 
(в тоннах). Не вычисляя интеграл, оценить нагрузку на узел.
Так как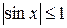 
, то при 
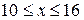справедлива оценка для подынтегральной функции 
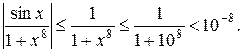Тогда, по свойствам 7) и 10), интеграл оценивается 
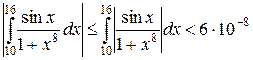. Отсюда видно, что нагрузка на узел не превосходит 
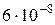тонн или 0,06 грамм, значит эта нагрузка незначительна и ее можно не учитывать.
