Геометрический смысл сумм Дарбу

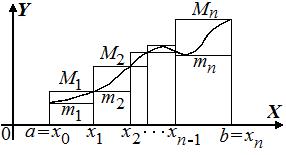
Верхняя интегральная сумма Дарбу 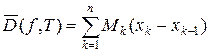равна площади ступенчатой фигуры, внутри которой лежит криволинейная трапеция.

Нижняя интегральная сумма Дарбу 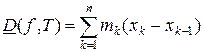задаёт площадь ступенчатой фигуры, которая содержится внутри криволинейной трапеции. Для непрерывной функции при измельчении разбиения площади обеих этих ступенчатых фигур стремятся к площади криволинейной трапеции.

Теорема (критерий интегрируемости Риману).

Функция интегрируема по Риману на отрезке , тогда и только тогда, когда для любого сколь угодно малого 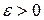, найдётся разбиение 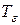, такое, что разность .

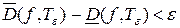Доказательство.

Необходимость.

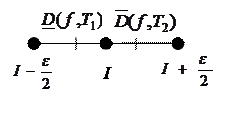Пусть функция интегрируема на отрезке . Тогда верхний интеграл Римана совпадает с нижним и выполняется равенство

.

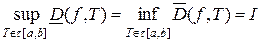Зафиксируем .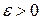

По определению точной верхней грани для .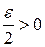

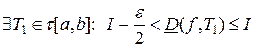По определению точной нижней грани для .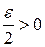

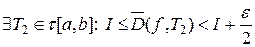Построим новое разбиение 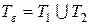, состоящее из всех точек как разбиения 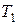, так и разбиения 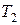. Разбиение 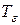является более мелким, чем каждое из разбиени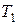й и 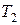. Поскольку при измельчении разбиения верхние суммы Дарбу не увеличиваются, а нижние суммы Дарбу не уменьшаются, то

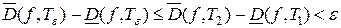. Значит, разбиение 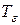является искомым.

Достаточность.

Пусть .

Докажем, что для функции верхний интеграл совпадает с нижним интегралом. Из определения точных верхней и нижней граней следует неравенство .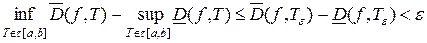

Отсюда получаем оценку для разности верхнего и нижнего интегралов

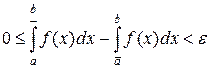. Так как число 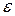произвольно мало, то

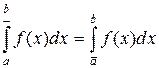и функция интегрируема по Риману, что и требовалось доказать.