Пусть функция  непрерывна на отрезке
непрерывна на отрезке  .
.
Функция 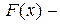 любая из первообразных функции
любая из первообразных функции  .
.
Тогда 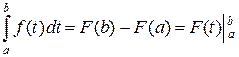 .
.
Доказательство. Из теоремы 2 следует, что интеграл с переменным верхним пределом является первообразной функции  . Поскольку
. Поскольку 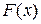 также является первообразной и две различные первообразные отличаются только на константу, то
также является первообразной и две различные первообразные отличаются только на константу, то 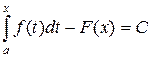 . (1)
. (1)
Найдем костанту С. Положим в последнем равенстве 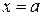 :
:
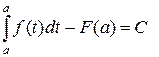 . Отсюда находим значение константы
. Отсюда находим значение константы 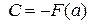 . Подставив его в равенство (1), получаем
. Подставив его в равенство (1), получаем
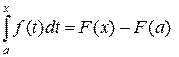 .
.
Полагая в этом равенстве 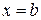 , получаем искомую формулу
, получаем искомую формулу 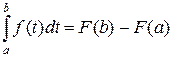 .
.
7.2. Правило интегрирования по частям в определённом интеграле.
Пусть функции 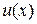 и
и 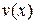 имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке  . Тогда справедлива формула интегрирования по частям
. Тогда справедлива формула интегрирования по частям
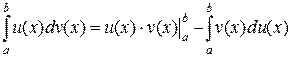 .
.
Пример 1. Вычислить интеграл 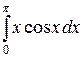 .
.
Обозначим через
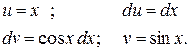
Подставляя эти выражения в формулу интегрирования по частям, получаем
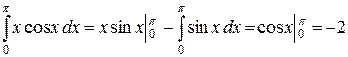 .
.
Пример 2. Вывести рекуррентную формулу для вычисления интеграла
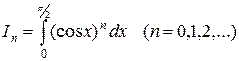 .
.
Обозначим через
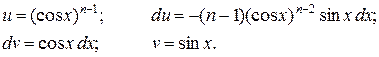
Подставляя эти выражения в формулу интегрирования по частям, получаем
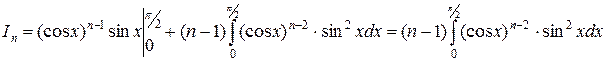 .
.
Воспользовавшись основным тригонометрическим тождеством 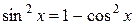 , сводим вычисление данного интеграла к таким же интегралам меньшего порядка
, сводим вычисление данного интеграла к таким же интегралам меньшего порядка
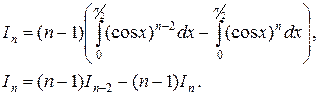
Отсюда находим рекуррентную формулу для вычисления искомого
интеграла 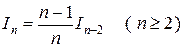 .
.
Начальные значения интегралов для этой формулы 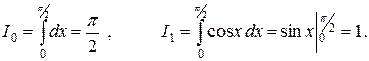
Пример 3. Вычислить интегралы 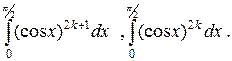
Применим рекуррентную формулу, выведенную в примере 2, при 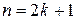 :
:
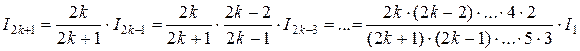 .
.
Учитывая, что 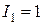 , получаем
, получаем 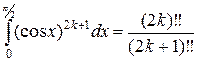 .
.
Применим рекуррентную формулу, выведенную в примере 2, при 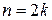 :
:
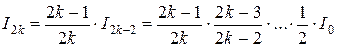 .
.
Учитывая, что 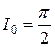 , получаем
, получаем 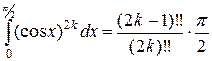 .
.
7.3. Замена переменной в определённом интеграле.
Пусть функция 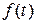 определена и непрерывна на отрезке
определена и непрерывна на отрезке 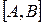 .
.
Функция 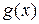 определена и непрерывна вместе со своей производной на отрезке
определена и непрерывна вместе со своей производной на отрезке  , причем
, причем 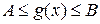 ,
, 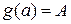 ,
, 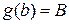 . Тогда справедлива формула замены переменной
. Тогда справедлива формула замены переменной
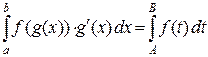 , где
, где 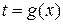 .
.
Пример 1. Вычислить интеграл 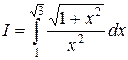 .
.
Первый способ. Перепишем подынтегральную функцию в виде
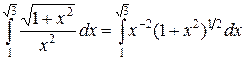 .
.
Этот интеграл является интегралом от дифференциального бинома
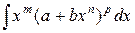 . В данном примере
. В данном примере 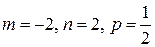 .
.
Число 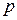 не является целым; число
не является целым; число 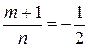 также не является целым;
также не является целым;
число 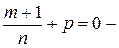 целое. Значит, исходя из общей теории, подходит подстановка
целое. Значит, исходя из общей теории, подходит подстановка 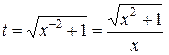 .
.
Возводим в квадрат и выражаем подынтегральные выражения
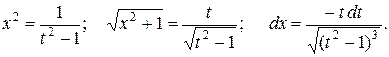
Пересчитаем пределы интегрирования из формулы  :
:
при 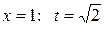 ; при
; при 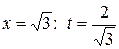 .
.
Подставляя эти выражения в первоначальный интеграл, получаем
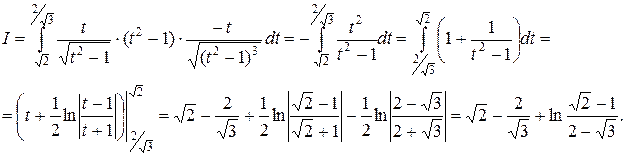
Второй способ. В этом интеграле можно избавиться от иррациональности с помощью тригонометрической подстановки. Сделаем замену
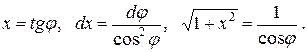
Пересчитаем пределы интегрирования. Если 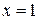 , то
, то 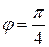 ;
;
если 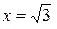 , то
, то 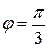 . Подставляя эти значения в интеграл, получаем
. Подставляя эти значения в интеграл, получаем
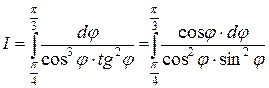 .
.
Сделаем еще одну замену переменной 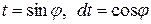 .
.
Если 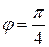 , то
, то 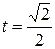 ; если
; если 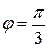 , то
, то 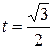 . Тогда
. Тогда
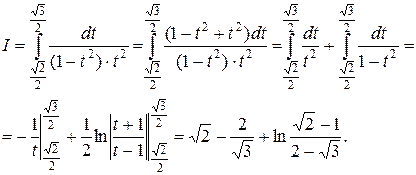
Отметим два основных отличия замены переменной в определённом интеграле от замены переменной в неопределённом интеграле:
1) надо пересчитывать пределы интегрирования;
2) не нужно возвращаться к старой переменной.
Следующий пример показывает, что формальное применение формулы замены переменной, без учета условий ее применимости, может привести к неверному результату.
Пример 2. Интеграл 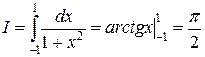 . Сделаем в этом интеграле замену
. Сделаем в этом интеграле замену 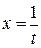 . Тогда
. Тогда 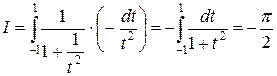 . Получили противоречие, так как один и тот же интеграл не может принимать два разных значения.
. Получили противоречие, так как один и тот же интеграл не может принимать два разных значения.
Это произошло потому, что при изменении переменной 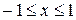
новая переменная 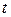 изменяется на лучах
изменяется на лучах 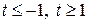 . А согласно теореме о замене переменной она должна изменяться на отрезке
. А согласно теореме о замене переменной она должна изменяться на отрезке 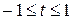 .
.
При замене переменной определенный интеграл Римана может перейти в несобственный интеграл и наоборот. Поэтому введем понятие несобственного интеграла. Позднее этот интеграл будет изучаться более подробно.
7.4. Несобственный интеграл
Интеграл Римана рассматривается от ограниченной функции на отрезке. Этот интеграл можно обобщить в двух направлениях: сделать неограниченным промежуток или функцию неограниченной.
Несобственный интеграл первого рода – это интеграл по неограниченому промежутку. Пусть функция  интегрируема по Риману в собственном смысле на любом отрезке
интегрируема по Риману в собственном смысле на любом отрезке  при всяком значении
при всяком значении 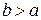 . Несобственным интегралом от функции
. Несобственным интегралом от функции  по лучу
по лучу 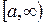 называется следующий предел от определенного интеграла
называется следующий предел от определенного интеграла
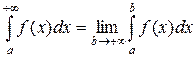 .
.
Возможны следующие случаи. Если предел существует и конечен, то говорят, что несобственный интеграл сходится.
Если же предел равен бесконечности или вообще не существует, то говорят, что несобственный интеграл расходится.
Пример 1. Исследовать на сходимость в зависимости от параметра 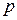 несобственный интеграл
несобственный интеграл 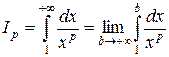 .
.
Рассмотрим сначала случай, когда 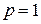 .Тогда
.Тогда
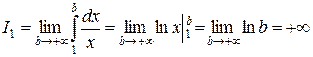 .
.
В этом случае интеграл расходится.
Пусть теперь 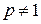 . Тогда
. Тогда
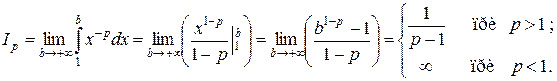
Итак, 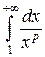 сходится при
сходится при 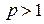 и расходится при
и расходится при 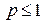 .
.
Это важный интеграл, он широко используется при исследовании на сходимость других несобственных интегралов, а также в теории рядов.
Пример 2. Исследовать на сходимость несобственный интеграл 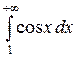 .
.
Запишем несобственный интеграл по определению
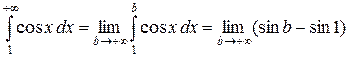 .
.
Полученный предел не существует, следовательно, интеграл расходится.
 2015-05-05
2015-05-05 2712
2712
