Классы интегрируемых функций

Необходимое условие интегрируемости – ограниченность функции. Суммы Дарбу можно составить только для ограниченных функций, так как величины 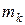и 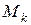не определены в случае неограниченности функции.

Условие ограниченности функции не является достаточным для её интегрируемости. Есть функции ограниченные, но не интегрируемые.

Пример функции, не интегрируемой по Риману на отрезке .

Рассмотрим функцию Дирихле, которая в рациональных точках отрезка принимает значение 1, а в иррациональных точках отрезка принимает значение 0:

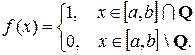
Очевидно, что эта функция ограниченна. Покажем, что она не является интегрируемой.

Пусть 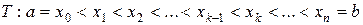– произвольное разбиение отрезка . В силу свойства всюду плотности множества рациональных чисел во множестве действительных чисел, в каждом частичном отрезке разбиения найдется рациональное число, поэтому верхние суммы Дарбу для любого разбиения равны .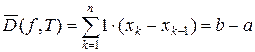

Отсюда верхний интеграл Римана равен .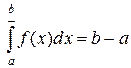

Поскольку иррациональные числа также обладают свойством всюду плотности во множестве действительных чисел, то для любого разбиения нижние суммы Дарбу равны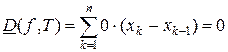

и, следовательно, нижний интеграл Римана .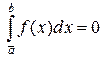

Поскольку для функции Дирихле верхний интеграл Римана не совпадает с нижним интегралом, то функция Дирихле не интегрируема по Риману.

Достаточные условия интегрируемости по Риману могут быть различными.

Теорема 1 (достаточное условие интегрируемости).

Если функция непрерывна на отрезке , то она интегрируема по Риману на этом отрезке.

Доказательство. Покажем, что функция интегрируема по Риману

по критерию интегрируемости.

Зафиксируем 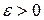и найдём разбиение 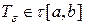такое, что .

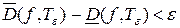Так как функция непрерывна на отрезке , то она равномерно непрерывна на нем. Тогда для числа

.

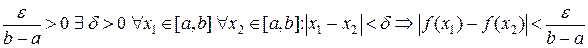Возьмём такое разбиение 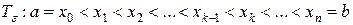, что мелкость разбиения 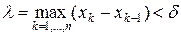. Покажем, что это разбиение будет искомым. Оценим разность между верхней и нижней суммами Дарбу

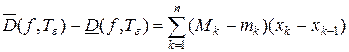, где .

Так как функция непрерывна на отрезке , то она непрерывна на каждом частичном отрезке 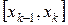, 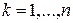. Поскольку непрерывная функция на отрезке достигает своих верхней и нижней граней, то

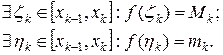
В силу равномерной непрерывности функции из того, что

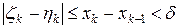, следует что .

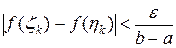Тогда разность между верхней и нижней суммами Дарбу оценивается как

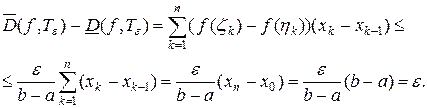
Итак, 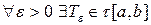, такое что 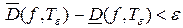. По критерию интегрируемости из этого следует, что функция интегрируема по Риману на отрезке , что и требовалось доказать.

Теорема 2 (достаточное условие интегрируемости).

Если функция определена на всем отрезке и возрастает на этом отрезке, то функция будет интегрируема по Риману на отрезке .

Доказательство. Покажем, что функция интегрируема по Риману

по критерию интегрируемости.

Зафиксируем 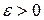и найдём разбиение 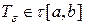такое, что .

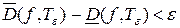Возьмём такое разбиение 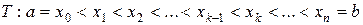, что мелкость разбиения .

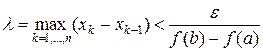Так как функция возрастает, то

.

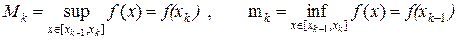Тогда разность между верхней и нижней суммами Дарбу оценивается как

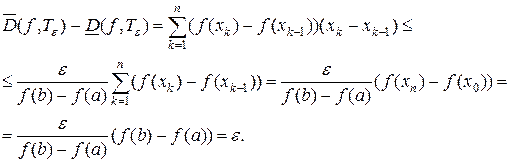
Итак, для любого 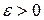нашли разбиение 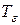, такое, что разность между верхней и нижней суммами Дарбу, соответствующими этому разбиению, меньше 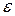. Тогда функция интегрируема по критерию интегрируемости.

Пример. Рассмотрим функцию, заданную формулами

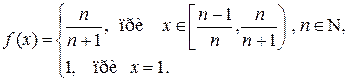
Функция определена и возрастает на всем отрезке 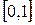. Тогда, по теореме 2 она будет интегрируема на нем, хотя имеет бесконечное число точек разрыва.

Критерий Лебега интегрируемости функции по Риману.

Функция интегрируема по Риману на отрезке тогда и только тогда, когда множество её точек разрыва можно покрыть системой конечного или счётного числа интервалов, сумма длин которых меньш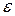е , где 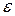- сколь угодно малое число.