Пусть тело ограничено плоскостями 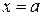 и
и 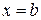 . Пусть каждое сечение тела плоскостью
. Пусть каждое сечение тела плоскостью 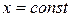 есть квадрируемая фигура
есть квадрируемая фигура 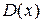 , причем ее площадь
, причем ее площадь 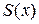 является непрерывной функцией на отрезке
является непрерывной функцией на отрезке 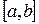 . Тогда тело будет кубируемо и его объем вычисляется по формуле
. Тогда тело будет кубируемо и его объем вычисляется по формуле 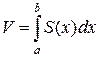 .
.
Доказательство.
Рассмотрим разбиение отрезка  конечным набором точек
конечным набором точек
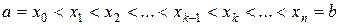 . Тогда
. Тогда 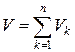 , где
, где 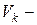 объём части тела, заключённой между плоскостями
объём части тела, заключённой между плоскостями 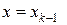 и
и 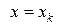 . В каждом частичном отрезке разбиения выберем точку
. В каждом частичном отрезке разбиения выберем точку 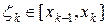 . Сечение тела плоскостью
. Сечение тела плоскостью 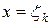 есть квадрируемая фигура
есть квадрируемая фигура 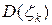 . Площадь
. Площадь 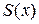 – непрерывная функция, следовательно, если отрезок
– непрерывная функция, следовательно, если отрезок 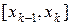 достаточно мал, то
достаточно мал, то 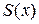 на нем изменяется мало, значит можно считать, что
на нем изменяется мало, значит можно считать, что 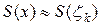
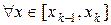 . Тогда объем
. Тогда объем 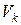 приблизительно равен объему призмы с площадью основания
приблизительно равен объему призмы с площадью основания 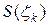 и высотой
и высотой 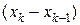 .Учитывая формулу объема призмы, получаем
.Учитывая формулу объема призмы, получаем 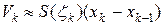 . Тогда объем всего тела приближенно равен
. Тогда объем всего тела приближенно равен 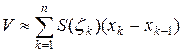 . Так как в правой части этого равенства стоит интегральная сумма Римана для функции
. Так как в правой части этого равенства стоит интегральная сумма Римана для функции 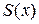 на отрезке
на отрезке  , то при мелкости разбиения
, то при мелкости разбиения 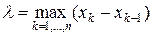 стремящейся к нулю, получаем формулу
стремящейся к нулю, получаем формулу 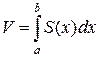 .
.
Пример. Найти объем эллипсоида.
Решение. Запишем уравнение эллипсоида: 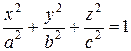 .
.
Найдем сечение эллипсоида плоскостью 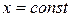 :
:
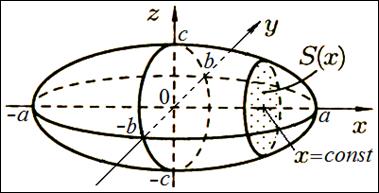
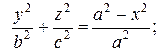
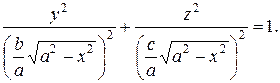
В сечении эллипсоида плоскостью 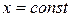 получился эллипс с полуосями
получился эллипс с полуосями
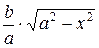 и
и 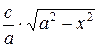 . Площадь этого эллипса равна
. Площадь этого эллипса равна
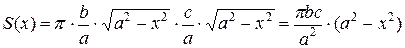 . Подставляя
. Подставляя 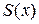 в формулу вычисления объема тела через площадь поперечных сечений, получаем
в формулу вычисления объема тела через площадь поперечных сечений, получаем

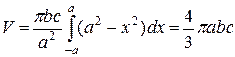 .
.
В частном случае, когда все полуоси эллипсоида одинаковы и равны 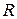 , получаем формулу объема шара
, получаем формулу объема шара 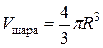 .
.
 2015-05-05
2015-05-05 4543
4543
