Криволинейный сектор – это фигура, ограниченная в полярных координатах лучами 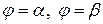 и графиком функции
и графиком функции 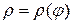 .
.
Теорема. Если функция 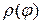 - непрерывна, то криволинейный сектор – квадрируемая фигура и площадь его находится по формуле
- непрерывна, то криволинейный сектор – квадрируемая фигура и площадь его находится по формуле
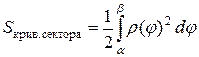 .
.
Доказательство.
Пусть 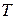 – разбиение отрезка
– разбиение отрезка 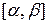 конечным набором точек
конечным набором точек
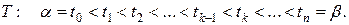
Тогда площадь криволинейного сектора разбилась на n частей. Обозначим через 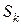 часть площади криволинейного сектора, ограниченного линиями
часть площади криволинейного сектора, ограниченного линиями 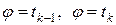 ,
, 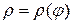 . Если мелкость разбиения
. Если мелкость разбиения 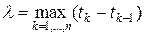 достаточно мала, то
достаточно мала, то 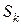 приближенно равна площади обычного кругового сектора с углом
приближенно равна площади обычного кругового сектора с углом 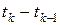 и радиусом
и радиусом 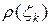 , где
, где 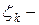 произвольная точка из интервала
произвольная точка из интервала 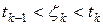 . Тогда верно приближенное равенство
. Тогда верно приближенное равенство 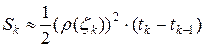 . А так как площадь криволинейного сектора равна
. А так как площадь криволинейного сектора равна 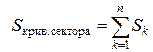 , то получаем приближенное равенство
, то получаем приближенное равенство
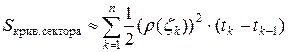 .
.
Здесь в правой части интегральная сумма Римана для функции 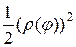 .
.
Поскольку функция 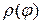 - непрерывна, то
- непрерывна, то 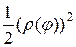 интегрируема и при
интегрируема и при 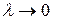 интегральные суммы стремятся к интегралу Римана. Таким образом получаем формулу
интегральные суммы стремятся к интегралу Римана. Таким образом получаем формулу 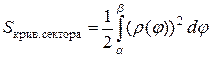 .
.
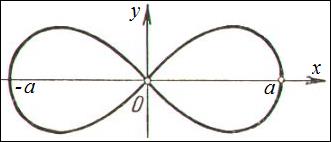 Пример. Найти площадь фигуры, ограниченной лемнискатой Бернулли, задаваемой уравнением
Пример. Найти площадь фигуры, ограниченной лемнискатой Бернулли, задаваемой уравнением 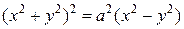 .
.
|
|
|
Перейдем к полярным координатам 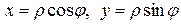 . Тогда уравнение кривой примет вид
. Тогда уравнение кривой примет вид 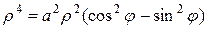 или
или 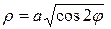 .
.
Найдем область определения функции из условия 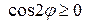 .
.
Решая это неравенство, находим 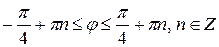 .
.
Функция имеет период 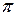 , значит ее график симметричен относительно начала координат.
, значит ее график симметричен относительно начала координат.
Так как 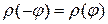 , то график функции также симметричен относительно оси
, то график функции также симметричен относительно оси  . В силу симметрии достаточно найти площадь части фигуры, расположенной в первой четверти
. В силу симметрии достаточно найти площадь части фигуры, расположенной в первой четверти 
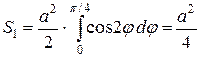 . Тогда площадь фигуры, ограниченной лемнискатой
. Тогда площадь фигуры, ограниченной лемнискатой 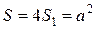 .
.
 2015-05-05
2015-05-05 1269
1269








