2015-05-05
2005
Телом назовём часть пространства, ограниченную замкнутой несамопересекающейся поверхностью. Понятие объема пространственного тела вводится аналогично понятию площади плоской фигуры.
Пусть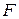 
– некоторое тело в пространстве. Его нижний объем определяется по формуле 
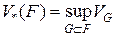, где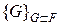 
– множество всех многогранников, лежащих внутри 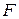. Верхний объем равен 
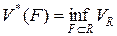, где 
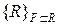– множество всех многогранников, содержащих в себе .
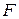Определение. Тело 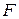кубируемо, если 
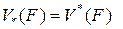, тогда объем тела равен 
.
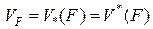Критерий кубируемости. Тело F кубируемо тогда и только тогда, когда для любого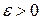 
найдутся многогранники 
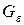и 
такие что 
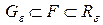и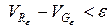 
.
Доказательство проводится аналогично доказательству критерия квадрируемости.
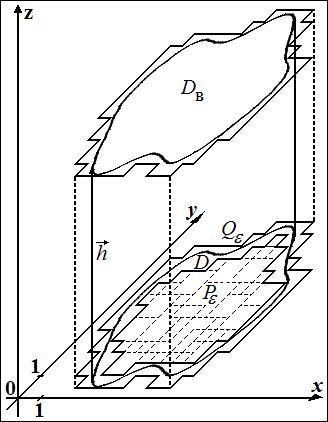
Пример. Пусть 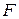- прямая призма, то есть тело, у которого верхнее основание 
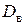получено из нижнего основания 
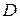сдвигом на вектор 
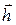, перпендикулярный нижнему основанию (при этом, конечно, фигуры 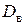и 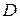равны). Докажем, что если основание 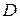квадрируемо, то сама призма 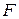кубируема, и ее объем вычисляется по формуле 
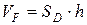, где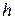 
– высота призмы, то есть длина вектора .
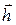Доказательство. Зафиксируем 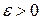. Так как фигура 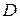квадрируема, то по критерию квадрируемости для 
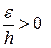найдутся многоугольники 
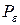и 
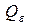такие, что 
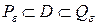и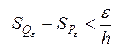 
. Многогранник с высотой 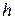и основанием 
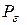лежит внутри призмы, а многогранник с основанием 
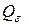и высотой 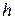содержит призму. Тогда разность объемов внешнего и внутреннего многогранников 
.
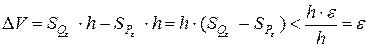Тогда, по критерию кубируемости, призма кубируема.
По определению объема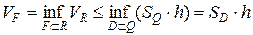 
. С другой стороны,
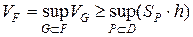. Отсюда видно, что 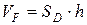, что и требовалось доказать.
