Пусть плоская фигура представляет собой криволинейную трапецию, верхняя граница которой задана параметрическими уравнениями
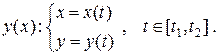
В этом случае площадь вычисляется по формуле
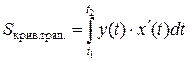 .
.
Пример. Вычислить площадь эллипса.
Зададим эллипс параметрическими уравнениями
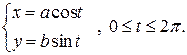
Поскольку эллипс симметричен относительно координатных осей, то можно искать площадь четверти эллипса, расположенной в первой координатной четверти. Эта фигура представляет собой криволинейную трапецию, у которой абсцисса меняется от 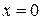 , что соответствует значению параметра
, что соответствует значению параметра 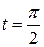 , до
, до 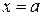 , что соответствует значению параметра
, что соответствует значению параметра 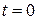 . Подставляя в формулу, находим
. Подставляя в формулу, находим
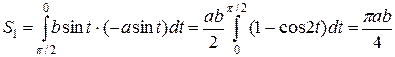 .
.
Отсюда площадь всего эллипса равна 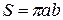 .
.
 2015-05-05
2015-05-05 1537
1537








