2015-05-05
5212
Рассмотрим поверхность, образованную вращением вокруг оси 
графика функции 
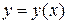, заданной на отрезке 
.
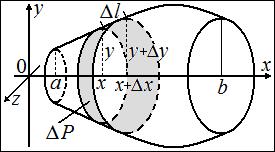
Найдём площадь малого элемента поверхности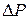 
. Площадь 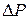приблизительно равна площади усечённого конуса, в основании которого круги радиуса 
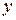и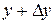 
, а образующая равна 
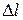. Площадь поверхности усеченного конуса с радиусом малого основания 
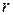, радиусом большого основания 
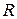и длиной образующей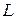 
вычисляется по формуле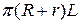 
. Поэтому 
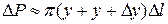. Отсюда 
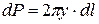, так как слагаемое 
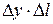, которое является бесконечно малой более высокого порядка, чем остальные слагаемые, можно отбросить. Для разных случаев задания кривой дифференциал длины дуги 
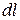записывается по-разному.
Если кривая задана явно, то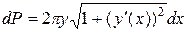 
и
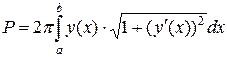– площадь поверхности вращения кривой, заданной явно уравнением , 
.
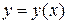В случае, если кривая задана параметрическими уравнениями
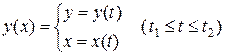, то
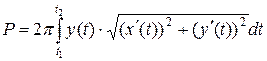– площадь поверхности вращения кривой, заданной параметрическими уравнениями.
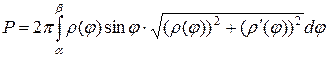– площадь поверхности вращения кривой, заданной в полярных координатах уравнением 
.
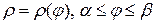Пример 1. Найти площадь шара радиуса .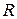
|
|
|
Поверхность шара можно получить вращением кривой, заданной уравнением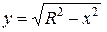 
, 
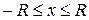. В силу симметрии можно считать площадь 
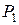половины поверхности, полученной вращением части окружности, лежащей в первой четверти.
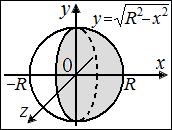Вычислим подынтегральные выражения:
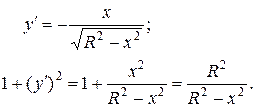
Подставляя их в формулу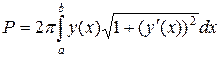 
площади поверхности кривой, заданной явными уравнениями,
получаем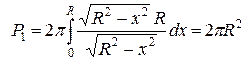 
.
Умножая на два, находим площадь поверхности шара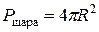 
.
Пример 2. Найти площадь поверхности, образованной вращением одной арки циклоиды вокруг оси .
Запишем параметрические уравнения циклоиды
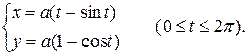
Найдем производные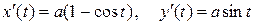 
. Упростим выражение
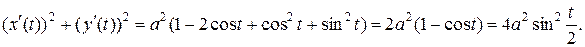
Подставляя его в формулу 
, получаем
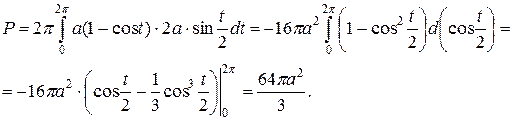
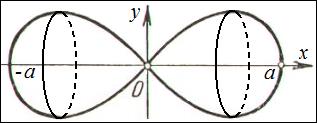
Пример 3. Найти площадь поверхности, полученной вращением
лемнискаты Бернулли вокруг оси .
Запишем уравнение лемнискаты в полярных координатах:
.
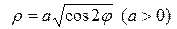В силу симметрии можно искать площадь половины поверхности. Она получается
при вращении части кривой, соответствующей значению аргумента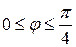 
.
Воспользуемся формулой
.
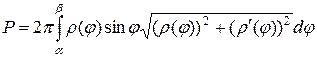Производная от функции равна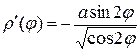 
.
Упростим подкоренное выражение
.
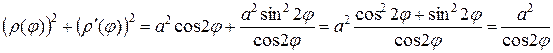Подставляя в формулу, находим площадь половины поверхности
.
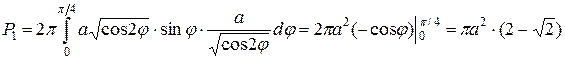Удваивая этот результат, получаем окончательный ответ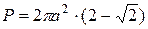 
.
8.5. Некоторые физические приложения определенного интеграла
