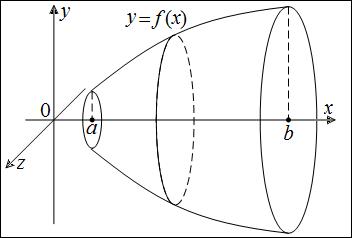
 Рассмотрим тело, которое получается при вращении криволинейной трапеции, ограниченной сверху графиком функции
Рассмотрим тело, которое получается при вращении криволинейной трапеции, ограниченной сверху графиком функции 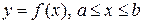 , вокруг оси
, вокруг оси  . Для вычисления его объема применим общую формулу объема тела через площадь поперечных сечений. В данном случае в сечении плоскостью
. Для вычисления его объема применим общую формулу объема тела через площадь поперечных сечений. В данном случае в сечении плоскостью 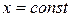 получается круг радиуса
получается круг радиуса 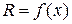 . Тогда его площадь
. Тогда его площадь 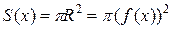 . Соответственно
. Соответственно
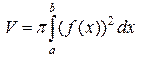 – объем тела вращения вокруг оси
– объем тела вращения вокруг оси  .
.
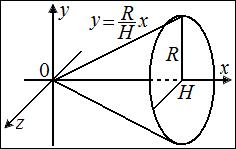
Пример. Найти объём конуса радиуса 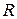 и высотой
и высотой  .
.
Конус – это тело, которое можно получить вращением вокруг оси  криволинейной трапеции под графиком линейной функции
криволинейной трапеции под графиком линейной функции 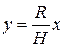 , где
, где 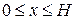 . Подставляя
. Подставляя 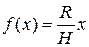 в формулу объема тела вращения, получаем
в формулу объема тела вращения, получаем
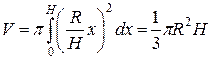 .
.
В случае вычисления объема тела, полученного вращением вокруг оси  фигуры под графиком функции, заданной параметрическими уравнениями
фигуры под графиком функции, заданной параметрическими уравнениями 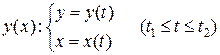 , формула имеет вид
, формула имеет вид 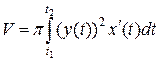 .
.
Пример. Найти объём тела, полученного вращением астроиды вокруг оси  .
.
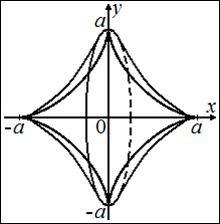
Параметрические уравнения астроиды
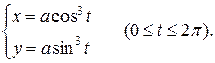
Так как кривая симметрична относительно обеих координатных осей, то можно считать только половину объема тела – это объем тела, полученного вращением части кривой, соответствующей изменению параметра
от 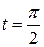 до
до 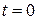 . Подставив в формулу вычисления объема, получим
. Подставив в формулу вычисления объема, получим 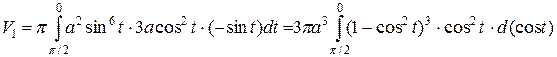 .
.
Сделаем в этом интеграле замену 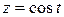 .
.
Пересчитаем пределы интегрирования: при 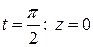 ; при
; при 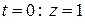 . Отсюда:
. Отсюда:
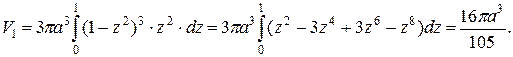
Удваивая полученный результат, получаем окончательный ответ 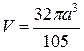 .
.
 2015-05-05
2015-05-05 3180
3180
