Обозначим maxDxi – наибольший отрезок разбиения, а minDxi – наименьший. Если maxDxi® 0, то число отрезков разбиения отрезка [a, b] стремится к бесконечности.
Если 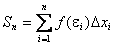 , то
, то 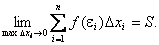
Определение: Если при любых разбиениях отрезка [a, b] таких, что maxDxi® 0 и произвольном выборе точек ei интегральная сумма 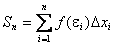 стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].
стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].
Обозначение: 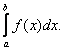
а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования.
Определение: Если для функции f(x) существует предел 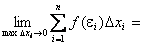
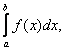 то функция называется интегрируемой на отрезке [a, b].
то функция называется интегрируемой на отрезке [a, b].
Также верны утверждения: 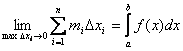
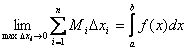
Теорема: Если функция f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.
Свойства определенного интеграла.
1) 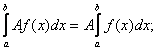
2) 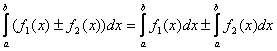
3) 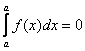
4) Если f(x) £ j(x) на отрезке [a, b] a < b, то 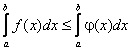
5) Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то:

6) Теорема о среднем. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка e такая, что
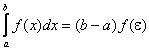
Доказательство: В соответствии со свойством 5:
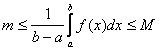
т.к. функция f(x) непрерывна на отрезке [a, b], то она принимает на этом отрезке все значения от m до М. Другими словами, существует такое число eÎ [a, b], что если
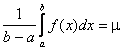 и m = f(e), а a £ e £ b, тогда
и m = f(e), а a £ e £ b, тогда 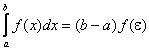 . Теорема доказана.
. Теорема доказана.
7) Для произвольных чисел a, b, c справедливо равенство:
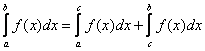
8) 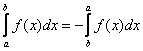
Обобщенная теорема о среднем. Если функции f(x) и j(x) непрерывны на отрезке [a, b], и функция j(х) знакопостоянна на нем, то на этом отрезке существует точка e, такая, что
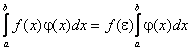
3. Определенный интеграл. Основные методы интегрирования.
Определенным интегралом функции 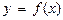 на отрезке
на отрезке  называется предел интегральной суммы при стремлении к нулю длины наибольшего «элементарного» отрезка:
называется предел интегральной суммы при стремлении к нулю длины наибольшего «элементарного» отрезка:
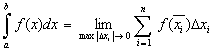
где 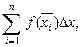 - интегральная сумма для функции
- интегральная сумма для функции 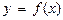 на отрезке
на отрезке 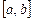 ; n – число «элементарных» отрезков, на которые разбивается отрезок
; n – число «элементарных» отрезков, на которые разбивается отрезок 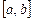 ;
; 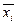 - произвольная точка внутри отрезка
- произвольная точка внутри отрезка 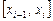 , длина которого равна
, длина которого равна 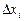 .
.
Основные свойства определенного интеграла
1°. При перестановке пределов интегрирования интеграл меняет знак на противоположный:
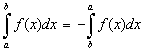
2°. Каковы бы ни были числа а, b, с, имеет место равенство
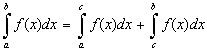
3°. Постоянный множитель можно выносить за знак определенного интеграла:
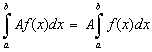
4°. Определенный интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций:
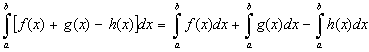
5°. Теорема о среднем значении. Определенный интеграл от непрерывной функции равен произведению длины промежутка интегрирования на значение подынтегральной функции при некотором промежуточном значении аргумента
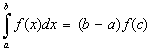
где 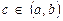 .
.
6о. Если 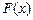 - какая-либо первообразная от непрерывной функции
- какая-либо первообразная от непрерывной функции 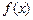 , то справедлива формула Ньютона - Лейбница
, то справедлива формула Ньютона - Лейбница
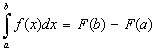
Вычисления определенных интегралов
a). Основным способом вычисления определенных интегралов является определение первообразной для подынтегральной функции и использование формулы Ньютона-Лейбница, которая может быть записана в виде
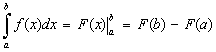
b). Замена переменной в определенном интеграле 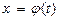 осуществляется по следующей формуле
осуществляется по следующей формуле
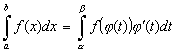
где 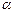 и
и 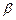 определяются в силу замены из условий
определяются в силу замены из условий 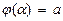 и
и 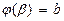 . Следует отметить, что при замене переменной в определенном интеграле, в отличие от замены переменной в неопределенном интеграле, возвращаться к старой переменной после замены не надо.
. Следует отметить, что при замене переменной в определенном интеграле, в отличие от замены переменной в неопределенном интеграле, возвращаться к старой переменной после замены не надо.
c). Формула интегрирования по частям для определенного интеграла имеет вид
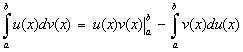
Рекомендации по выбору u и dv остаются точно такими же, как и для формулы интегрирования по частям в неопределенном интеграле.
В задании 6 необходимо вычислить определенный интеграл. В некоторых случаях необходимо воспользоваться заменой переменной в определенном интеграле, в других - формулой интегрирования по частям.
Задание 6. Вычислить определенный интеграл с точностью до двух знаков после запятой
a). 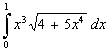 , b).
, b). 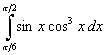 , c).
, c). 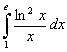 ,
,
d). 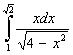 , e).
, e). 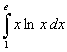 , f).
, f). 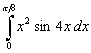 .
.
Решение: В заданиях a), b), c), d) выполним или замену переменной или внесение под знак дифференциала. В заданиях e), f) применим формулу интегрирования по частям.
Задание 6 a). 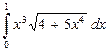 .
.
Воспользуемся методом замены переменной. Введем новую переменную t по формуле 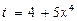 . Тогда
. Тогда 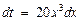 или
или 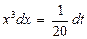 . Осуществим пересчет пределов интегрирования, используя вид замены. Подставим нижний предел интегрирования старой переменной
. Осуществим пересчет пределов интегрирования, используя вид замены. Подставим нижний предел интегрирования старой переменной 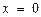 в выражение
в выражение 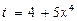 и найдем нижний предел интегрирования новой переменной
и найдем нижний предел интегрирования новой переменной 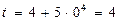 . Аналогично, подставляя верхний предел интегрирования старой переменной
. Аналогично, подставляя верхний предел интегрирования старой переменной 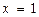 , найдем верхний предел интегрирования новой переменной
, найдем верхний предел интегрирования новой переменной 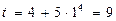 . Тогда
. Тогда
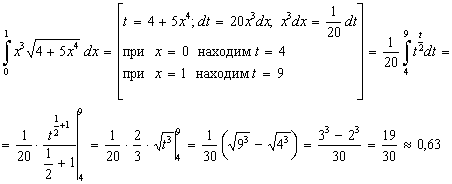
Отметим, что предложенный пример можно было вычислить, используя метод внесения под знак дифференциала (можно было внести под знак дифференциала 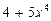 ). В этом случае пересчет пределов интегрирования не осуществляется. Этот метод будет проиллюстрирован в следующем примере.
). В этом случае пересчет пределов интегрирования не осуществляется. Этот метод будет проиллюстрирован в следующем примере.
Задание 6 b). 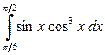 .
.
Воспользуемся методом внесения под знак дифференциала. Внесем под знак дифференциала функцию 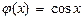 . Так как
. Так как
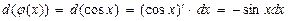 ,
,
то получим
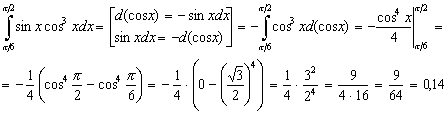
Задание 6 с). 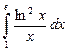 .
.
Воспользуемся методом замены переменной. Введем новую переменную t по формуле 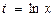 . Тогда
. Тогда 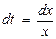 . Осуществим пересчет пределов интегрирования. При
. Осуществим пересчет пределов интегрирования. При 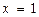 получим
получим 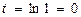 . При
. При 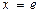 получим
получим 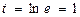 . Тогда получим
. Тогда получим
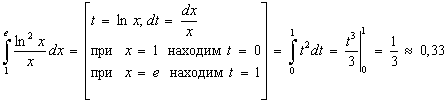
Задание 6 d). 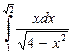 .
.
Воспользуемся методом внесения под знак дифференциала. Внесем под знак дифференциала функцию 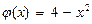 .
.
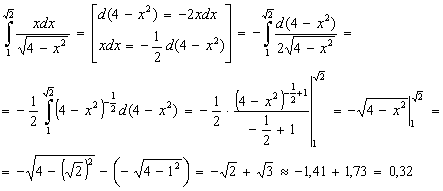
Задание 6 e). 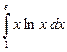 .
.
Применим формулу интегрирования по частям для определенного интеграла. Данный интеграл является интегралом II типа.
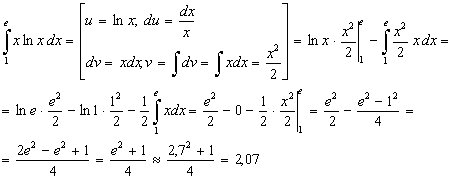
Задание 6 f). 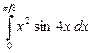 .
.
Применим формулу интегрирования по частям для определенного интеграла два раза, так как под знаком интеграла стоит многочлен второй степени. Данный интеграл является интегралом I типа.
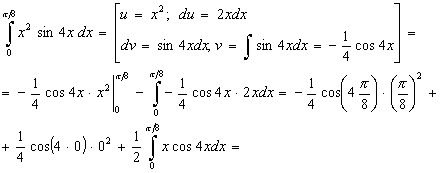
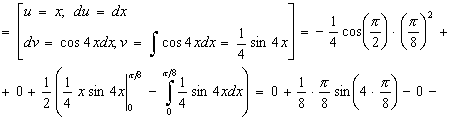
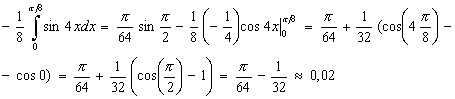
 2015-05-05
2015-05-05 551
551