Интегрируемость непрерывной функции

Теорема:

Если функция y=f(x) непрерывна на отрезке [ a, b ], то она интегрируема на этом отрезке.

Доказательство:

Так как функция f(x) непрерывна на [ a, b ], то она равномерно непрерывна на этом отрезке. Тогда по следствию из теоремы Кантора, отрезок [ a, b ] можно разбить на конечное число частей так, что на каждой из них колебание w_i функции будет меньше , w_i< (1). Составим для данного разбиения суммы Дарбу и рассмотрим разность 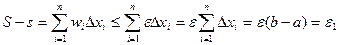(2).

Так как - любое, сколь угодно малое число, то и 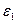тоже сколь угодно мало. Итак, для любого 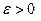, существует 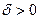, что если наибольший из отрезков разбиения λ<δ, то выполняется неравенство .

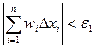Это означает, что 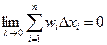, а это значит, что функция интегрируема на отрезке [ a, b ].