Теорема:
Если функция f(x) ограничена на [ a, b ] и имеет на нем конечное число точек разрыва, то она интегрируема на этом отрезке.
Доказательство:
Можем считать, не нарушая общности, что на [ a, b ] существует только одна точка разрыва х /. Возьмем произвольное число  >0 и окружим точку х /
>0 и окружим точку х /  - окрестностью. На отрезке [ a, х /-
- окрестностью. На отрезке [ a, х /-  ] функция непрерывна, следовательно для данного
] функция непрерывна, следовательно для данного  можно указать такое
можно указать такое 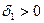 , что если [ a, х/-
, что если [ a, х/-  ] разбить на части с длинами, меньшими δ1, то колебание функции на каждой из этих частей будет меньше
] разбить на части с длинами, меньшими δ1, то колебание функции на каждой из этих частей будет меньше  . Аналогично для отрезка [ х /+
. Аналогично для отрезка [ х /+  , b ] можно указать
, b ] можно указать 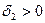 , такое что, если этот отрезок разбить на части с длинами меньшими
, такое что, если этот отрезок разбить на части с длинами меньшими 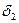 , то колебание функции на каждой из частей будет меньше
, то колебание функции на каждой из частей будет меньше  . Из δ1 и δ2 выберем наименьшее и обозначим его δ0. Тогда, если отрезок [ a, х /-
. Из δ1 и δ2 выберем наименьшее и обозначим его δ0. Тогда, если отрезок [ a, х /-  ] и [ х /+
] и [ х /+  , b ] разбить на части с длинами, меньшими δ, то колебание функции на каждой из частей будет меньше
, b ] разбить на части с длинами, меньшими δ, то колебание функции на каждой из частей будет меньше  . Кроме того, мы можем взять
. Кроме того, мы можем взять 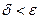 . Разобьем отрезок [ a, b ] на части с длинами, меньшими δ.
. Разобьем отрезок [ a, b ] на части с длинами, меньшими δ.
Тогда получим отрезки двух типов:
1 тип – отрезки, целиком лежащие вне окрестности;
2 тип – отрезки либо целиком лежащие в окрестности, либо частично попадающие в нее.
Так как функция ограничена, то колебания функции на каждом промежутке не превосходят колебаний функции на всем [ a, b ]. Обозначим его Ω. Разобьем сумму 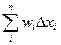 на две суммы
на две суммы 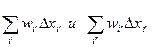 , соответствующие отрезкам 1 и 2 типов.
, соответствующие отрезкам 1 и 2 типов.
Имеем: 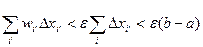 .
.
Заметим, что длины всех отрезков, целиком лежащих в окрестности точки х /, меньше 2  . Длины отрезков частично попадающих в окрестность, а их не более двух, меньше 2δ < 2
. Длины отрезков частично попадающих в окрестность, а их не более двух, меньше 2δ < 2  .
.
Для второй суммы имеем: 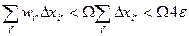 .
.
Тогда
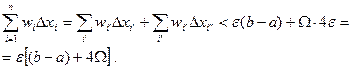
Показано, что 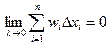 .
.
Последнее равенство говорит о том, что функция интегрируема.
 2015-05-05
2015-05-05 3502
3502








