2015-05-05
3174
1°. Если a > b, то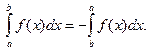 
Если a=b, то принимается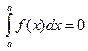 
для любой функции. е
2°. Определенный интеграл не зависит от обозначения переменной интегрирования, то есть
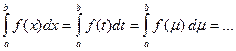
3°. Если функция f(x) интегрируема на большем из трех отрезков [ a, b ], [ a, c ], [ c, b ], то она интегрируема на двух оставшихся, и при этом, имеет место равенство:
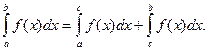
(Данное равенство не зависит от взаимного расположения точек a, b, c).
Доказательство:
1) Рассмотрим случай, когда a < c < b.
 |
По условию f(x) интегрируема на [ a, b ]. По определению интеграла имеем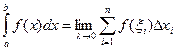 
, причем этот предел не зависит от способа деления отрезка [ a, b ] на части и выбора точек 
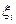. Поэтому можем разбить [ a, b ] на части так, чтобы точка с всегда была точкой деления:
.
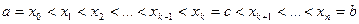Тогда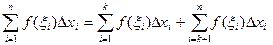 
. Первая из этих сумм соответствует разбиению отрезка
[ a, c ], вторая – [ с, b ]. Переходя к пределу при наибольшем из отрезков разбиения l→0, получим:
.
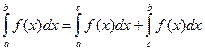2) Рассмотрим теперь другое расположение точек. Например, a < b < c.
Тогда по доказанному выше
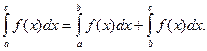
Отсюда
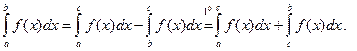
4°. Если функция f(x) интегрируема на отрезке [ a, b ], то и функция k f(x), где k=сonst также будет интегрируема на этом отрезке и при этом
.
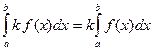Докажите это утверждение самостоятельно, используя определение .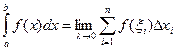
5°. Если функции f(x) и g(x) интегрируемы на отрезке [ a, b ], то и их алгебраическая сумма f(x) ± g(x) также интегрируема на этом отрезке, причем
.
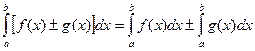Докажите это утверждение самостоятельно, используя
определение .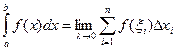
6°. Пусть функция f(x) интегрируема на отрезке [ a, b ], где a < b и пусть при этом f(x) ³ 0,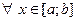 
, тогда
.
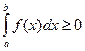Доказательство:
Составим интегральные суммы
.
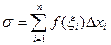Заметим, что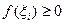 
по условию, а так как a < b, то и 
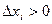. Поэтому и суммы 
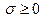. Переходя к пределу интегральных сумм при l→0, получим, что и
.
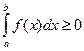Аналогично доказывается, что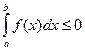 
, если f(x) £ 0,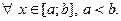 
7°. Пусть функции f(x) и g(x) интегрируемы на отрезке [ a, b ],
где a < b,и при этом, f(x) £ g(x), тогда
.
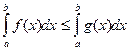Доказательство:
На основании свойства 5° функция f(x) - g(x) интегрируема на [ a, b ] и, кроме того, f(x) - g(x)£ 0, a < b. Тогда по свойству 6°
.
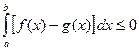Применяя к левой части последнего неравенства свойство 5°, получим
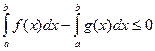. Откуда и следует утверждение
.
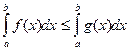8°. Пусть функция f(x) интегрируема на отрезке [ a, b ], где
a < b, тогда и функция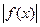 
также интегрируема на этом отрезке, и имеет место неравенство
.
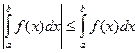Доказательство:
Из свойств абсолютной величины следует, что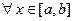 
имеют место неравенства 
.
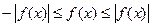Проинтегрируем и воспользуемся свойством 7°, получим:
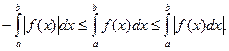
То есть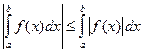 
.
(Здесь мы учли, что неравенства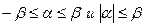 
равносильны.)
9°. Пусть функция f(x) интегрируема на отрезке [ a, b ], где
a < b, и при этом f(x) удовлетворяет неравенству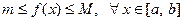 
. Тогда
.
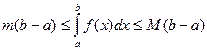Доказательство:
Разобьем отрезок [ a, b ] произвольным образом на n частей, очевидно, что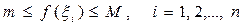 
. Умножим обе части этого неравенства на 
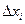. Так как a < b, то 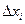>0, и знаки неравенств не изменятся:
.
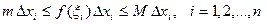Просуммировав, получим:
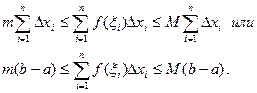
Переходя к пределу при l→0, получим требуемое:
.
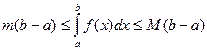10°. Теорема о среднем значении функции:
Если функция f(x) интегрируема на отрезке [ a, b ] и удовлетворяет на этом отрезке неравенствам m £ f(x) £ M, то существует число μ, m £ m £ M, такое, что
.
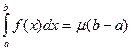Доказательство:
1) Пусть a < b, тогда по свойству 9°
.
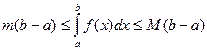Разделим все части неравенств на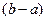 
>0:
.
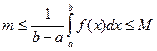Обозначим число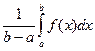 
за m,
то есть m =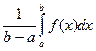 
.
Тогда m £ m £ M и .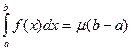
2) Пусть теперь b < a. Тогда по доказанному выше
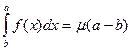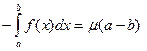или
или .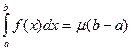
Следствие: Если функция f(x) непрерывна на отрезке [ a, b ], то на этом отрезке найдется хотя бы одна точка с, такая что
.
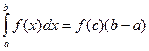Доказательство:
Так как функция f(x) непрерывна на отрезке [ a, b ], то по второй теореме Вейерштрасса она достигает на этом отрезке своего наибольшего М и наименьшего m значений. Это значит, что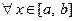 
, m £ f(x) £ M. В этом случае выполнены все условия теоремы о среднем, и по этой теореме найдется число m, m £ m £ M, такое что
.
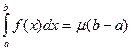Так как m - промежуточное значение между m и M, а f(x) непрерывна на отрезке [ a, b ], то по второй теореме Больцано-Коши найдется хотя бы одна точка с, такая что f(с)=m. Подставив это в последнее равенство, получим:
.
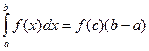Замечание: Теорема о среднем в исходной формулировке допускает следующее геометрическое истолкование.
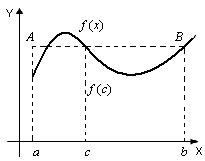
Пусть f(x) ³ 0 на [ a, b ].
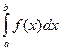численно равен площади криволинейной трапеции.
Рассмотрим прямоугольник abBA с тем же основанием, что и у криволинейной трапеции, и высотой, равной значению функции, определенному по теореме о среднем. Произведение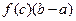 
численно равно площади прямоугольника abBA. Следовательно, криволинейная трапеция равновелика прямоугольнику с тем же основанием, а высотой, равной значению подынтегральной функции в «средней» точке с.
