В неопределенном интеграле формула интегрирования по частям имеет вид 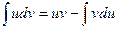 , где u, v – функции от независимой переменной х, непрерывные в рассматриваемом промежутке [ a, b ] вместе со своими производными.
, где u, v – функции от независимой переменной х, непрерывные в рассматриваемом промежутке [ a, b ] вместе со своими производными.
Аналогичная формула имеет место и в определенном интеграле.
Действительно, так как 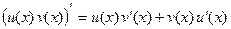 ,
,
то функция 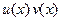 является первообразной для функции
является первообразной для функции
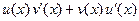 (по определению).
(по определению).
Тогда по формуле Ньютона-Лейбница
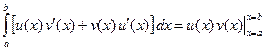 .
.
По свойству аддитивности определенного интеграла относительно подынтегральной функции имеем:
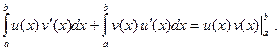
Следовательно
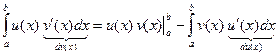
или
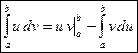
Примеры. Вычислить интегралы:

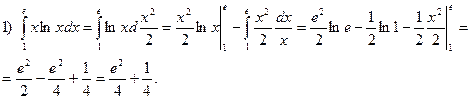
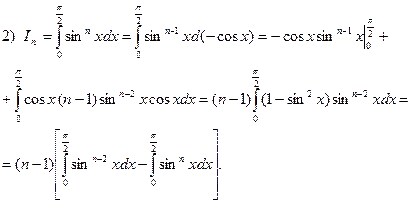
Итак, 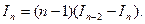
Приведя подобные, получим: 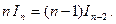
Таким образом рекуррентная формула имеет вид
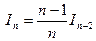 . (*)
. (*)
Если индексы четные:
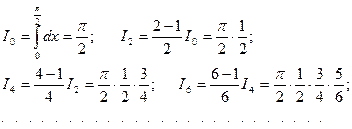
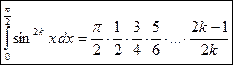
Если индексы нечетные, то:
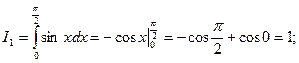
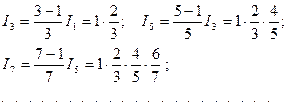
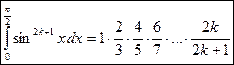
Ниже будет показано, что 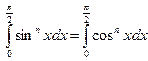 .
.
 2015-05-05
2015-05-05 562
562








