Признак сходимости несобственных интегралов I рода

Теорема:

Пусть функции f(x) и g(x) непрерывны в (а, ∞) и для всех х из этого бесконечного интервала выполняются неравенства 0 < f(x) £ g(x). Тогда из сходимости несобственного интеграла 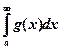следует сходимость интеграла 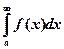, а из расходимости интеграла 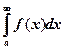следует расходимость интеграла .

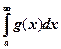Докажем предварительно леммы.

Лемма 1. Если функция j (х) возрастает, и предел j (х) при х→∞ равен А, то j (х)£ А.

Доказательство:

.

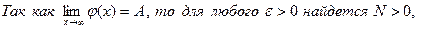
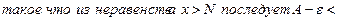
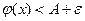Допустим противное, что нашлось такое числ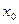о , что 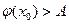. Если 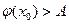, то можно выбрать e настолько малым, что 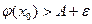. Если же возьмем 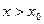, то это неравенство также будет выполняться, то есть 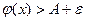(в силу возрастания функции j (х)).

Если возьмем 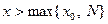, то с одной стороны 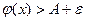, а с другой – для любого e 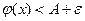. Получили противоречие, которое доказывает лемму.

Лемма 2. Если функция j (х) возрастает в интервале (а, ∞) и ограничена сверху, то существует конечный предел функции j (х) при х→∞.

Доказательство:

Рассмотрим множество значений функции 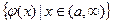. Это множество по условию ограничено сверху, следовательно существует 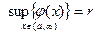, что означает:

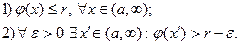
Если рассмотреть х>x^/, то и для них, в силу возрастания функции j (х), .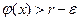

Итак, для любого 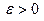существует 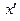, что для всех 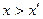выполняются неравенства 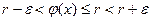, то есть существует .

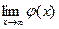Доказательство теоремы (признак сравнения несобственных интегралов):

Пусть 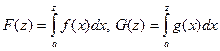. Отметим, как ведут себя эти функции. Так как подынтегральные функции положительны, то функции F(x) и G(x) возрастают на (a; +∞).

Так как, по условию интеграл 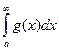сходится, то существует 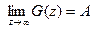. Из возрастания функции G(z), в силу леммы 1, 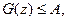для любого 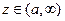. Учитывая данные в условии теоремы неравенства и 7⁰ свойство определенного интеграла, .

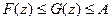Следовательно 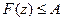и F(z) возрастает. По лемме 2 существует предел 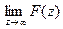, то есть 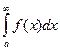сходится.

Последнее предложение в формулировке теоремы доказывается методом от противного.