(область интегрирования бесконечна)
Выясним, что представляют собой интегралы вида:
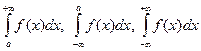 .
.
Пусть функция y=f(x) непрерывна на бесконечном промежутке [ а, +∞). Что понимать под интегралом 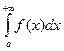 ?
?
Рассмотрим интеграл 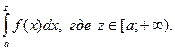 Он представляет собой функцию от z. Может случиться, что
Он представляет собой функцию от z. Может случиться, что
при 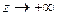 эта функция имеет предел.
эта функция имеет предел.
 Опр. Под интегралом
Опр. Под интегралом 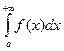 понимается
понимается 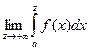 .
.
Если предел существует и он конечный, то 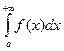 называется сходящимся несобственным интегралом, равным этому пределу. В противном случае говорят, что несобственный интеграл
называется сходящимся несобственным интегралом, равным этому пределу. В противном случае говорят, что несобственный интеграл 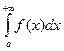 расходится.
расходится.
Если F(x) первообразная для f(x), то 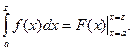
Тогда 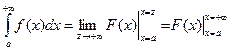
Аналогично определяется интеграл 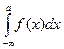 .
.
 Опр. Несобственный интеграл
Опр. Несобственный интеграл 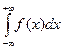 называется сходящимся, если сходится каждый из интегралов
называется сходящимся, если сходится каждый из интегралов 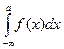 и
и 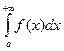 .
.
Пример. Вычислить несобственные интегралы
1) 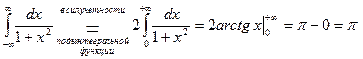 .
.
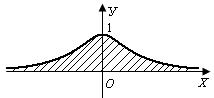
Геометрически данный интеграл представляет площадь бесконечной фигуры, лежащей под локоном Аньези 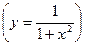 выше оси ОХ.
выше оси ОХ.
2) 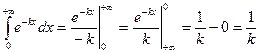 .
.
3) Вычислим интеграл, который будет нужен в теории рядов.
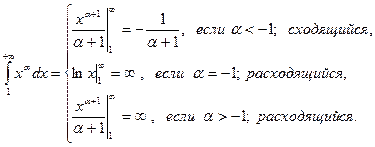
 2015-05-05
2015-05-05 550
550








