(подынтегральная функция неограничена)
Неограниченные на отрезке функции могут вести себя по-разному, например:
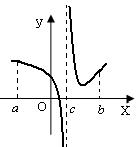
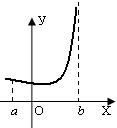
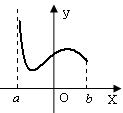
Достаточно изучить случай, когда разрыв только в одном конце отрезка (если разрыв в двух концах, то разбить на два интеграла).
Пусть функция f(x) интегрируема на отрезке [ a, b-e ] при любом как угодно малом e>0, но неограниченна на
[ b-e, b ].
 Опр. Если существует конечный предел
Опр. Если существует конечный предел 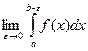 , то говорят, что несобственный интеграл II рода
, то говорят, что несобственный интеграл II рода 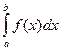 с особенностью в точке b сходится.
с особенностью в точке b сходится.
При этом величину предела принимают за величину несобственного интеграла: 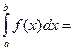
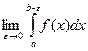 .
.
Если особенность в точке а, то 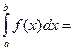
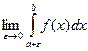 .
.
Пример:
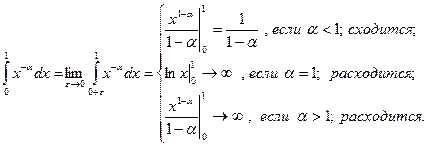
Для несобственных интегралов II рода справедлив признак сравнения, аналогичный признаку сравнения для несобственных интегралов I рода.
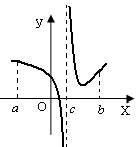
Если рассматривать несобственный интеграл II рода с особенностью во внутренней точке с, то нужно рассмотреть 2 интеграла с пределами от а до с-e1, и от с+e2 до b:
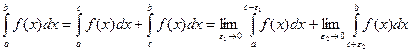 .
.
 2015-05-05
2015-05-05 576
576








