Абсолютно сходящиеся несобственные интегралы

(первого и второго рода)

Опр. Несобственный интеграл 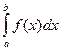называется абсолютно сходящимся, если сходится соответствующий несобственный интеграл от абсолютной величины данной функции, то есть .

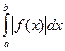Из этого определения еще не ясно, является ли абсолютно сходящийся интеграл, сходящимся.

Теорема:

Если несобственный интеграл сходится абсолютно, то он сходится.

Дано: 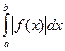- сходится.

Доказать: 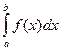- сходится.

Доказательство:

Рассмотрим функции: .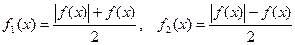

Сравним эти функции с 0 и с :

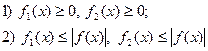
Таким образом:

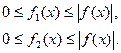
Тогда по признаку сходимости несобственных интегралов, 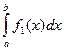и 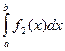сходятся, следовательно сходится и интеграл 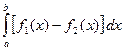. 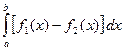= 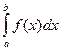, значит 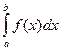- сходится, что и требовалось доказать.