Теорема (о достаточных условиях дифференцируемости):
Пусть:
1) В некоторой окрестности точки 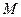
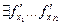
2) В самой точке 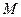
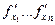 - непрерывны.
- непрерывны.
Тогда: 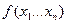 дифференцируема в точке
дифференцируема в точке 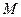 .
.
Определение: Пусть функция 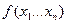 дифференцируема в точке
дифференцируема в точке 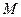 .
.
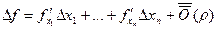 =
= 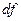 .
.
Главная линейная относительно 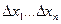 часть приращения функции
часть приращения функции 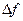 называется полным первым дифференциалом функции
называется полным первым дифференциалом функции 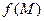 .
.
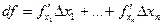
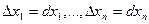
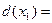
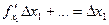
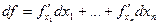
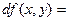
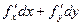
Величины 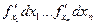 называются частичными дифференциалами
называются частичными дифференциалами 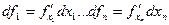
 2015-05-05
2015-05-05 237
237








