Билет 7

Замечание: 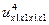- несмешанная производная 4-го порядка. Если же среди переменных, по которым берутся производные, есть хотя бы 2 различные, то такая производная называется смешанной.

Пример: 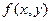. 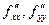- несмешанные производные. 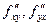- смешанные производные.

Теорема (о равенстве смешанных производных):

Есть функция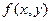

Пусть:

1) в некоторой окрестности точки 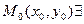частные производные .

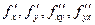2) 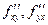непрерывны в точке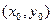

Тогда 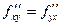в точке .

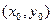Следствие:

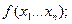
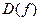. Пусть 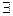и непрерывны все частные производные до 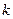-го порядка включительно в области 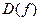. Тогда смешанные производные до 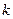-го порядка не зависят от порядка дифференцирования.