ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ТЕОРЕМЫ.
БИЛЕТ 1.
Определение (предел на языке 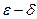 )
)
Пусть точка 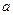
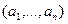 - точка сгущения множества
- точка сгущения множества 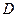 =
= 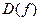 (не обязательно
(не обязательно  . Пусть
. Пусть 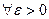
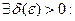
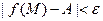 . Лишь только
. Лишь только 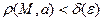 . Тогда говорят, что в точке
. Тогда говорят, что в точке 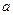 существует предел
существует предел 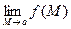 и он равен
и он равен 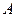 .
.
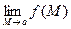 =
= 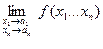 =
= 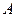
Определение: 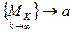 , если
, если 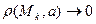 при
при 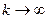 . Очевидно, можно записать и так:
. Очевидно, можно записать и так:
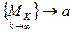 , если
, если 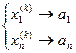 .
. 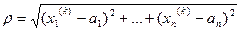 .
.
Определение: (предел 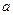 на языке последовательностей).
на языке последовательностей).
Пусть точка 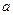
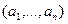 - точка сгущения множества
- точка сгущения множества 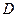 . Пусть
. Пусть 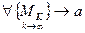 выполнено
выполнено 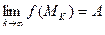 . Тогда говорят, что
. Тогда говорят, что 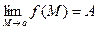 :
:
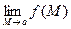 =
= 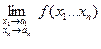 =
= 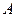
Два определения предела эквивалентны.
БИЛЕТ 2.
Непрерывные функции.
Пусть 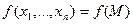 .
. 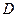 =
= 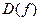 .
. 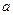 - внутренняя точка множества
- внутренняя точка множества 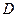 (точка сгущения)
(точка сгущения)
Определение 1.
Пусть выполнено:
1) 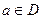 ,
, 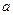 -внутренняя точка
-внутренняя точка
2) 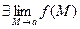
3) 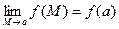
Тогда функция 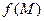 называется непрерывной в точке
называется непрерывной в точке 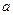
Определение 2: (непрерывность на языке 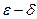 )
)
1)Пусть 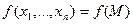 .
. 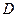 =
= 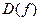 .
. 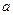 - внутренняя точка множества
- внутренняя точка множества 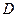 (точка сгущения)
(точка сгущения)
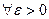
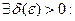
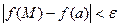 . Тогда функция
. Тогда функция 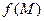 называется непрерывной в точке
называется непрерывной в точке 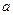
Определение 3: (непрерывность на языке последовательностей)
1) Пусть точка 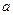
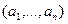 - точка сгущения множества
- точка сгущения множества 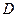 .
.
2) Пусть 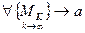 выполнено
выполнено 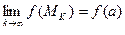 .
.
Тогда функция 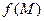 называется непрерывной в точке
называется непрерывной в точке 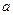
Определение 4: (непрерывность на языке приращений)
Пусть 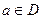 ,
, 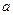 - внутренняя точка множества
- внутренняя точка множества 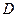 ,
, 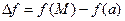 ,
, 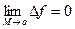 . Тогда функция
. Тогда функция 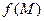 называется непрерывной в точке
называется непрерывной в точке 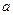
 2015-05-05
2015-05-05 238
238







