Билет 4

Определение: Функция 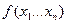называется дифференцируемой в точке 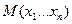, если ее полное приращение в этой точке представимо в виде: 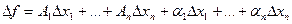, (х)

Где 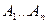-некоторые числа, независящие от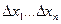

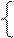
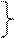
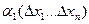
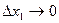
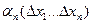- бесконечно малые при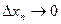

Утверждение: равенство (х) можно записать в эквивалентном виде (хх):

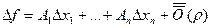(хх), где .

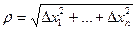То есть 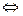(х) (хх)

Утверждение: Пусть функция 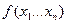дифференцируема в точке 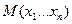. Тогда в точке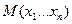 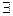частные производные по всем переменным и они равны :

,…, .

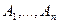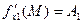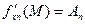Утверждение: Если функция 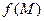дифференцируема в точке 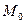, то она непрерывна в этой точке.