Билет 12

Теорема (без доказательства):

Пусть

1) определена и непрерывна в некоторой окрестности точки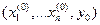

2)

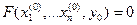
3) существуют и непрерывны все частные производные первого порядка: 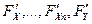в точке

.

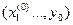4). 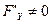в точке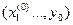

Тогда существует окрестность точки .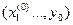

а) уравнение 2) определяет однозначную функцию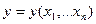

б)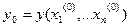

в) 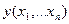- непрерывна в этой окрестности

г) существуют непрерывные частные производные 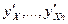в этой окрестности.

Определение: данная матрица называется матрицей Якоби системы функций 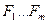по переменным .

.

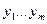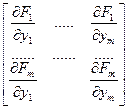Теорема:

Пусть

1) в некоторой окрестности точки 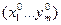функции 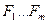определены и непрерывны.

2)

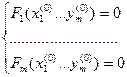
3) Существуют и непрерывны частные производные 1-го порядка по всем переменным:

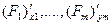в этой окрестности.

Тогда существует окрестность точки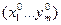

а) система уравнений (х) определяет 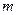однозначных неявных функций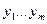

б)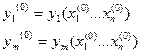

в) 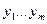- непрерывные функции от переменных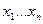

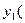
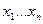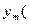
г) ),…, )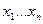- дифференцируемы в этой окрестности.

Замечание: (2) 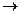(в) сохранили в) для единообразия.