Решение. Каноническое уравнение прямой линии в пространстве имеет вид

Каноническое уравнение прямой линии в пространстве имеет вид:

,

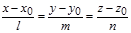где 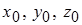– координаты любой точки, лежащей на прямой;

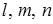– координаты направляющего вектора прямой, т.е. координаты любого не нулевого вектора, параллельного прямой.

В уравнении плоскости 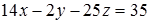коэффициенты при переменных x, y, z являются координатами вектора 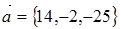, перпендикулярного плоскости и, следовательно, параллельного искомой прямой. Таким образом, уравнение прямой, проходящей через точку M(2,5, –1) перпендикулярно плоскости a: 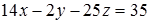, имеет вид:

.

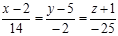Ответ: .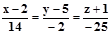

Вариант № 3.

Написать уравнение плоскости, проходящей через точки M(2; 4; 6), N(3; 1; – 4) и K(– 3; – 5; 1).