Уравнение плоскости имеет вид:
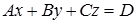 ,
,
где A, B, C – координаты вектора 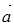 , перпендикулярного плоскости,
, перпендикулярного плоскости,
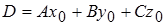 ,
,
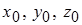 – координаты любой точки, лежащей на плоскости.
– координаты любой точки, лежащей на плоскости.
В качестве точки, лежащей на плоскости, возьмем точку M(2; 4; 6).
Векторы  и
и 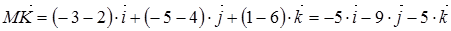 параллельны искомой плоскости, следовательно, их векторное произведение будет вектором
параллельны искомой плоскости, следовательно, их векторное произведение будет вектором 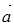 , перпендикулярным плоскости.
, перпендикулярным плоскости.
Вычислим вектор 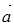 :
:
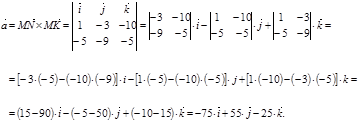
Вектор 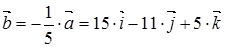 также будет перпендикулярным искомой плоскости.
также будет перпендикулярным искомой плоскости.
Вычислим величину D:
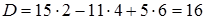 .
.
Таким образом, уравнение искомой плоскости имеет вид:
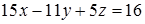 .
.
Ответ: 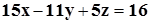 .
.
Вариант № 4.
Написать уравнение плоскости, проходящей через точку M(– 1; 1; 0) перпендикулярно прямой 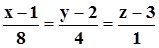 .
.
 2015-05-05
2015-05-05 340
340








