Определенное таким образом семейство плоскостей ограничивает вокруг узла обратной решетки, совмещенного с началом координат, некоторый объем, имеющий форму многогранника.
В случае простой кубической решетки многогранник является кубом. Его грани образованы плоскостями, проведенными через середины векторов, соединяющих данный узел решетки с его ближайшими соседями. Все остальные плоскости проходят дальше от узла и не участвуют в формировании граней куба.
В случае объемоцентрированной кубической решетки получается более сложный многогранник (см. ниже). Его грани образуются плоскостями, проведенными между данным узлом и его ближайшими и вторыми ближайшими соседями.
Построенный многогранник называется первой зоной Бриллюэна.
Если из всего объединения плоскостей удалить грани первой зоны Бриллюэна, то оставшееся множество ограничит новый, б\'ольший многогранник вокруг начала координат. Часть этого многогранника, не входящая в первую зону Бриллюэна, образует вторую зону Бриллюэна.
|
|
|
На следующем шаге мы получим третью зону Бриллюэна, и т. д.
На рис. 6 изображены четыре зоны Бриллюэна для двумерной прямоугольной обратной решетки. Строятся они также, как и в трехмерном случае, только вместо плоскостей проводятся прямые.
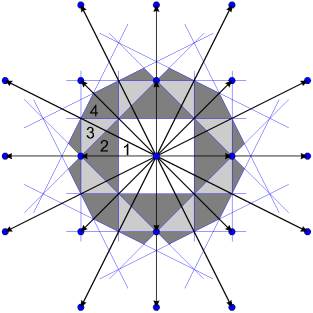 Рис. 6. Рис. 6. |
Теперь, после того как мы ввели понятие зон Бриллюэна, мы можем переформулировать условие рассеяния рентгеновской волны следующим образом: волна рассеивается, если конец ее волнового вектора лежит на границе некоторой зоны Бриллюэна.
В дальнейшем мы для простоты часто будем рассматривать одномерные решетки и нам придется иметь дело с одномерными зонами Бриллюэна.
Пусть прямая решетка имеет период a.
Понятие обратной решетки возникло из разложения периодической функции по плоским волнам. В одномерном случае разложение периодической функции в ряд Фурье имеет вид:
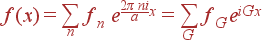 | (42) |
Таким образом, обратную решетку в одномерном случае образуют точки Gn = 2 π n / a, эти точки и играют роль векторов обратной решетки.
Зоны Бриллюэна строятся также, как и в трехмерном случае, но вместо плоскостей ставятся точки на середине отрезков, соединяющих узлы обратной решетки. Первая зона — отрезок [– π / a, π / a ], вторая — отрезок [–2 π / a,2 π / a ] за вычетом первой зоны, и т. д. (рис. 7)
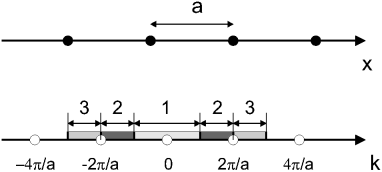 Рис. 7. Зоны Бриллюэна в одномерном случае. Рис. 7. Зоны Бриллюэна в одномерном случае. |
Первую зону Бриллюэна можно рассматривать как примитивную ячейку обратной решетки, обладающую точечной симметрией этой решетки. Действительно, если мы построим первую зону Бриллюэна вокруг каждого узла обратной решетки (поместив начало координат в этот узел), то такие зоны целиком заполнят все пространство, не перекрываясь при этом друг с другом. Отсюда, в частности, следует, что объем первой зоны Бриллюэна равен объему примитивной ячейки обратной решетки.
|
|
|
Некоторые свойства зон Бриллюэна:
Объем всех зон Бриллюэна одинаков и равен объему примитивной ячейки обратной решетки. Отсюда в частности следует, что зона Бриллюэна содержит столько разрешенных значений волновых векторов, сколько примитивных ячеек содержится в объеме кристалла (см. (36)).
Если к вектору обратного пространства 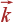 , конец которого лежит в первой зоне Бриллюэна, прибавить любой вектор обратной решетки, то полученный вектор выйдет за пределы первой зоны.
, конец которого лежит в первой зоне Бриллюэна, прибавить любой вектор обратной решетки, то полученный вектор выйдет за пределы первой зоны.
И наоборот, из любого вектора 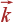 , конец которого не лежит в первой зоне Бриллюэна, можно путем вычитания некоторого вектора обратной решетки получить вектор, конец которого находится в пределах первой зоны.
, конец которого не лежит в первой зоне Бриллюэна, можно путем вычитания некоторого вектора обратной решетки получить вектор, конец которого находится в пределах первой зоны.
Таким образом, все зоны Бриллюэна являются репликами первой зоны: из можно получить, транслируя точки, принадлежащие первой зоне, на вектора обратной решетки.
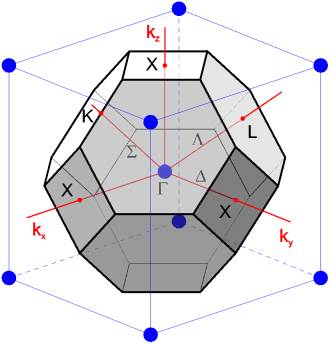 Рис. 8. Рис. 8. |
Большинство распространенных полупроводников имеют гранецентрированную кубическую (ГЦК) решетку Браве, поэтому посмотрим, как устроена первая зона Бриллюэна у этой решетки.
Обратная решетка в этом случае является объемоцентрированной кубической (ОЦК). Первая зона Бриллюэна изображена на рис. 8. Получается она, согласно описанному выше алгоритму, следующим образом.
Проведем сначала плоскости, делящие пополам отрезки между центральным узлом в кубической элементарной ячейке и его вторыми ближайшими соседями — центральными узлами в прилегающих кубических ячейках. Эти плоскости ограничат вокруг центрального узла куб, совпадающий с кубической ячейкой. По углам этого куба расположены ближайшие соседи центрального узла. Плоскости, проведенные между центральным узлом и этими соседями, при пересечении с кубом образуют шестиугольные грани, а на гранях куба ''вырежут'' квадраты.
Некоторые точки и линии высокой симметрии в первой зоне Бриллюэна ГЦК-решетки имеют общепринятые обозначения.
Центр зоны Бриллюэна обозначается греческой буквой Γ.
Точки на поверхности обозначаются латинскими буквами: X — центр квадратной грани (направление (1,0,0) в k -пространстве и эквивалентные ему, всего 6 точек); L — центр шестиугольной грани (направления (1,1,1) и эквивалентные, 8 точек); K — середина ребра между соседними шестиугольными гранями (направление (1,1,0) и эквивалентные, 12 точек).
Линии, соединяющие центр зоны с точками на поверхности обозначаются греческими буквами: Γ X — Δ (направления типа (1,0,0)), Γ L — Λ (направления типа (1,1,1)), Γ K — Σ (направления типа (1,1,0)).
 2015-05-05
2015-05-05 4498
4498








