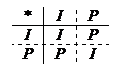 Рассмотрим группу G – группу симметрий трехмерного пространства, состоящего из трех элементов: I – тождественное преобразование и Р – отражение пространства относительно начала координат.
Рассмотрим группу G – группу симметрий трехмерного пространства, состоящего из трех элементов: I – тождественное преобразование и Р – отражение пространства относительно начала координат.
Т.е. G = { I, P }. При этом умножение элементов задано таблицей:
1) Одномерное представление группы G.
Пусть Е 1 – пространство представлений и е 1 – базис. Пусть линейный невырожденный оператор А (1) в этом базисе имеет матрицу А (1) = (1). Очевидно, это преобразование образует подгруппу в группе GL (1) причем умножение в этой подгруппе задается по правилу:
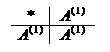 Мы получили одномерное представление D (1)(G) группы G
Мы получили одномерное представление D (1)(G) группы G
D (1)(I) = А (1); D (1)(P) = А (1);
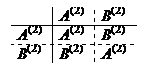 2) Двумерное представление группы G. Выберем в Е 2 базис { е 1, е 2} и рассмотрим в этом базисе матрицы преобразований:
2) Двумерное представление группы G. Выберем в Е 2 базис { е 1, е 2} и рассмотрим в этом базисе матрицы преобразований: 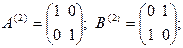 операции задаются таблицей:
операции задаются таблицей:
Получим двумерное представление группы G с помощью соотношений: D (2)(I) = А (2); D (2)(P)= В (2);
Этими соотношениями определяется изоморфизм группы G на подгруппу { A (2); B (2)} группы GL (2), т.е. это точное представление группы G.
1) Трехмерное представление группы G. Рассмотрим в Е 3 в базисе { е 1, е 2, е 3} линейное преобразование А (3) с матрицей А (3) = 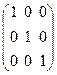 и законом умножения: А (3)× А (3) = А (3). Получаем трехмерное представление D (3)(G) с помощью соотношений:
и законом умножения: А (3)× А (3) = А (3). Получаем трехмерное представление D (3)(G) с помощью соотношений:
D (3)(I) = А (3); D (3)(P) = А (3).
4) Четырехмерное представление группы G. Рассмотрим в Е 4 линейные преобразования А (4) и В (4) с матрицами: 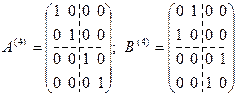 . Преобразования А (4) и В (4) образуют подгруппу в GL (4) с законом умножения, аналогичным примеру 2, соотношениями: D (4)(I) = А (4), D (4)(P) = В (4).
. Преобразования А (4) и В (4) образуют подгруппу в GL (4) с законом умножения, аналогичным примеру 2, соотношениями: D (4)(I) = А (4), D (4)(P) = В (4).
Заметив, что А (4) и В (4) можно записать в виде 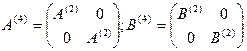 ,
,
можно записать (условно): D (4)(G) = D (2)(G) + D (2)(G) = 2 D (2)(G).
Аналогично можно условно записать D (3)(G) = 3 D (3)(G).
Используя это замечание можно без труда построить представление группы G любой конечной размерности.
 2015-05-05
2015-05-05 955
955








