Вывод интеграла Дюамеля

Пусть требуется определить ток в линейном пассивном двухполюснике, переходная характеристика которого известна, при включении двухполюсника на напряжение u. Кривая напряжения u изображена на рис.6.8. Начальный запас энергии двухполюсника считаем равным нулю.

Выберем некоторый произвольный фиксированный момент времени t и рассчитаем переходной ток к этому моменту времени. Хотя момент выбирается произвольно, он фиксируется и становится постоянной величиной - параметром. В связи с этим введем новое обозначение времени через τ, изменяющегося в пределах 0≤τ≤t. В дальнейшем будем различать u(t) и i(t), как функции момента наблюдения t и u(τ) и i(τ), как функции текущего времени τ.

Определим сначала ток в цепи при воздействии на цепь ступенчатого напряжения, приближенно заменяющего заданное плавное как это изображено на рис.6.8. Замена плавной кривой ступенчатой позволяет считать, что в момент времени τ=0 включается постоянное напряжение u(0)1(t), воздействующее на цепь в течение всего интервала времени от 0 до ∞. Затем через промежуток времени τ₁ вступает в действие дополнительное постоянное напряжение величиной Δu₁, воздействующее на цепь с момента времени τ₁. Затем вступает Δu₂ в момент времени τ₁ и т.д.

Заданное плавно изменяющееся напряжение приближенно представляется в виде u(0) и суммы большого числа последовательно включаемых элементарных скачков величиной Δu₁, Δu₂, … Δu_к до Δu_n, каждый их которых после включения действует в течение промежутка от τ_к до бесконечности. Под влиянием напряжения Δu(0) в цепи возникает переходный процесс. До момента наблюдения переходный процесс будет продолжаться t секунд. Под влиянием скачка Δu₁, включаемого в момент τ₁, в соответствии с принципом наложения возникает дополнительный переходный процесс. Продолжительность этого переходного процесса к моменту наблюдения t будет равна t-τ₁. Продолжительность переходного процесса, возникшего под влиянием скачка Δu_к до момент наблюдения t будет равна t-τ_к и т.д. Используя единичную функцию с запаздывающим аргументом, можно приближенно записать приложенное к цепи напряжение в виде суммы:

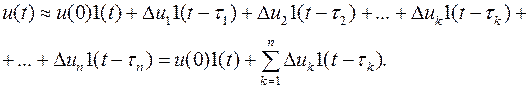(6.26)

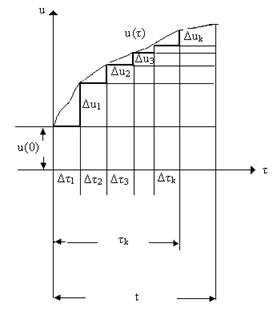
Рис.6.8

Реакция цепи (рассматриваемом случае – ток) определится как алгебраическая сумма реакций цепи на воздействия начального напряжения и всех последующих скачков напряжения, включаемых друг за другом. Под влиянием составляющей напряжения u(0)1(t) в цепи появится составляющая тока i(τ), которая к моменту наблюдения приобретет значение i(t)=u(0)g(t).

Спустя время τ₁, напряжение скачком возрастает на величину Δu₁. Продолжительность воздействия этого скачка напряжения равна t-τ₁, так как он включен с запаздыванием на t-τ₁. Поэтому отвечающая ему переходная характеристика будет g(t-τ₁). В результате в цепи появится добавочная составляющая тока Δi₁=Δu₁g(t-τ₁).

В последующий момент времени τ₂ (рис.6.8) вновь происходит скачкообразное изменение напряжения на величину Δu₂, которое вызовет вновь дополнительную составляющую тока: Δi₂=Δu₂g(t-τ₂).

Продолжая рассуждения, найдем, что в момент τ_к скачок напряжения Δu_к вызовет ток Δi_к=Δu_кg(t-τ_к).

Исходный переходный ток будет равен сумме составляющих, найденных для момента t, т.е.

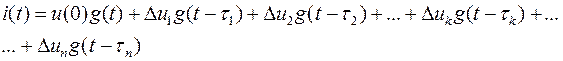
или

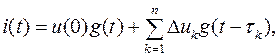
где n – число промежутков, на которое разбит интервал времени от 0 до t.

Для того чтобы получить выражение тока, соответствующее не ступенчатой кривой напряжения, а заданному плавно изменяющемуся напряжению, необходимо промежутки времени уменьшать до бесконечно малой величины dτ, а число скачков увеличивать до бесконечности (n→∞). Сами скачки пи этом будут бесконечно малыми величинами. Величина каждого скачка напряжения du можно представить в виде: du=u’(τ)dτ. Сумма в пределе перейдет в интеграл. Точное значение переходного тока i(t) для фиксированного времениt будет:

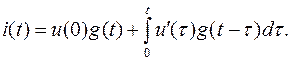(6.27)

Полученное выражение называется интегралом Дюамеля.

Для расчета тока по формуле (6.27) необходимо знать закон изменения заданного напряжения в аналитической форме и переходную характеристику цепи.

Интеграл Дюамеля записывают и в других формах. Если воспользоваться эквивалентным преобразованием интеграла вида свертки функций, т.е.

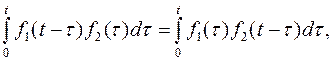то можно получить вторую форму записи интеграла Дюамеля

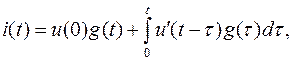(6.28)

где 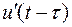- производная функции 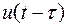по ее аргументу .

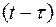Выполнив интегрирование по частям в первой форме записи интеграла Дюамеля (6.27), найдем третью форму записи:

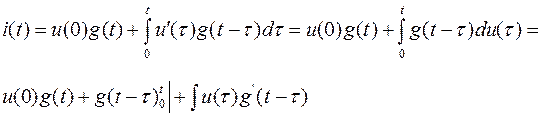
Подставляя пределы, получим

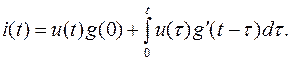(6.29)

Наконец, используя вновь эквивалентное преобразование интеграла в (6.29), получим четвертую форму интеграла:

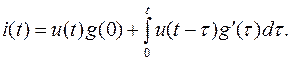(6.30)

Пользуясь правилом дифференцирования определенных интегралов по параметру, все четыре формулы записи интеграла Дюамеля (6.27) – (6.30) можно свести к двум:

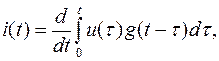(6.31)

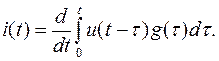(6.32)

Все четыре формы интеграла Дюамеля в теоретическом отношении равноценны. Ту или иную форму записи выбирают из соображений простоты вычислений, которые зависят от того, какой вид имеют функции u(t) и g(t).

Например, если u(0)=0, то удобнее первая (6.27) и вторая (6.28) формы записи, так как первое слагаемое в этих формах записи обращается в нуль. Если g(0)=0, то целесообразнее использовать третью или четвертую формы записи. Если g(t) выражается через экспоненциальную функцию, то следует предпочесть формулу (6.29) или (6.30), так как экспоненциальные функции просто дифференцируются.

Аналогично четыре формы интеграла Дюамеля можно записать для четырехполюсников, если заменить g(t) на k(t), i(t) на u₂(t), u(t) на u₁(t).