Спектр одиночного прямоугольного видеоимпульса (ОПВИ)

В связи с тем, что одиночный прямоугольный видеоимпульс (рис. 1.29) может быть представлен следующим образом

Рис.1.29

,

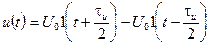то, используя свойство аддитивности преобразований Фурье, которое заключается в том, что если

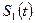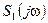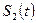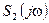≓ , ≓ и т. д., то

≓

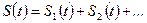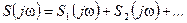
а также свойство сдвига аргумента состоящее в том, что если

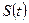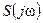≓ , то ≓ ,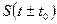

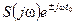получим:

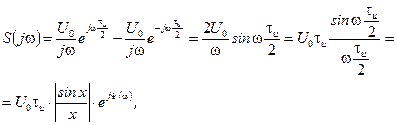
где 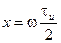, а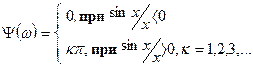

Аналогичное выражение для 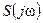одиночного прямоугольного видеоимпульса получим, применяя интеграл Фурье

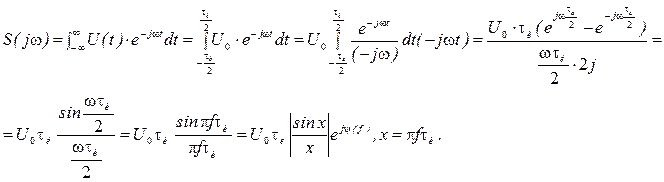
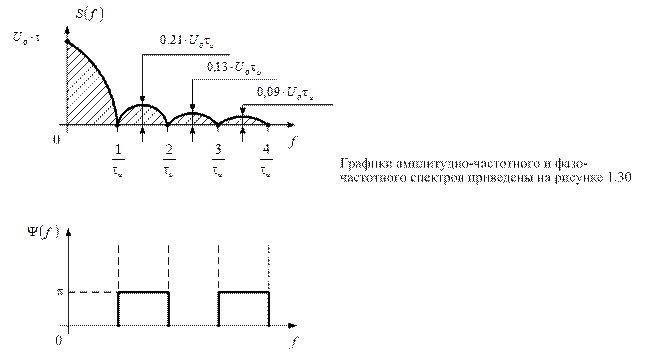
Рис.1.30

Спектральная плотность зависит от частоты в соответствии с функцией

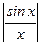
Максимальное значение спектральной плотности при .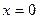

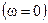Нулевые значения спектральной плотности будут иметь место на частотах 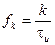, т.к. функция 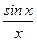проходит через ноль, когда 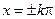, где 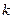= 1.2.3,.... т.е. на частотах

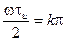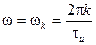, или .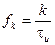

Ширина спектра сигнала, определяемая на уровне 90% энергии сигнала (Э_с) равна 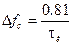. База сигнала .

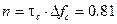График ФЧС построен исходя из следующих соображений. Положительным значением 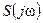соответствуют начальные фазы, равные нулю, а отрицательным - начальные фазы, равные .

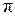Для оценки влияния длительности импульса на его спектр сравним АЧС импульсов разной длительности и одинаковой амплитуды. Длительность первого импульса 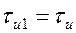, второго .

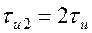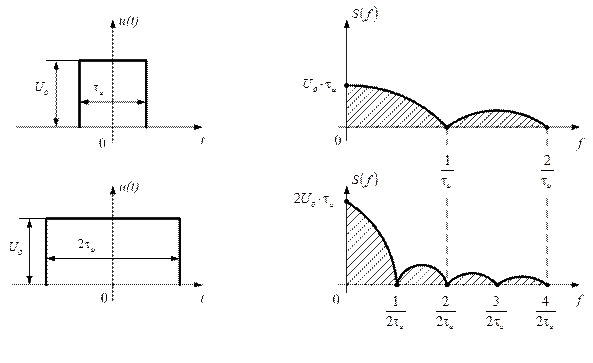
Рис. 1.31

Из анализа графиков рисунка 1.31 следует, что удлинению импульса в 2 раза соответствует сужение графика АЧС, при этом ширина спектра уменьшается в 2 раза 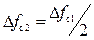, максимальное значение 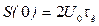пропорционально длительности импульса и увеличивается в 2 раза.

Для запаздывающего импульса, показанного на рисунке 1.6, спектральная плотность в соответствии с полученным выше результатом и теоремой о сдвиге аргумента будет

≓

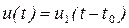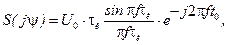
то есть при неизменном АЧС ФЧС определяется выражением

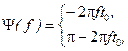
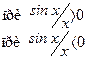
График ФЧС при 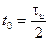показан на рисунке 1.32

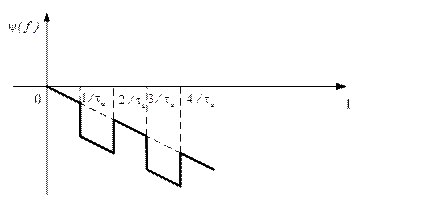
Рис.1.32