Спектр дискретного сигнала

15 16 17 18 19 20 21

Определим дискретный сигнал x_д(t) через совокупность отсчетов непрерывной функции x(t):

x(k)=x(t=kΔ) (1)

Тогда сам дискретный сигнал можно записать в виде модели:

x_д(t)=x(t)f_n(t), (2)

где 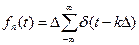безразмерная периодическая (с периодом Δ)

решетчатая функция.

Покажем, что дискретный сигнал (1) имеет спектр по Фурье вида:

(3)

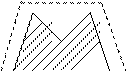
где Śx(f) - спектр исходного непрерывного сигнала x(t). Из (3) следует, что спектр дискретного сигнала повторяется с периодом частоты дискретизации Fд (см. рис.).

АЧХ ФНЧ Sx_д(f) спектр исходного сигнала

S_x(f)

₀

Fд Fд

-Fв +Fв

Амплитудный спектр первичного дискретного сигнала

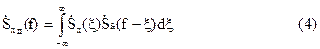Из математики известно (задача Парсеваля), что спектр Фурье от произведения двух функций определяется сверткой спектров сомножителей

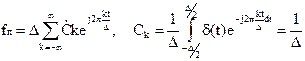где Ś_f_n(f) -- спектр по Фурье периодической функции f_n(t) c периодом Δ, которую представили комплексным рядом Фурье:

(при интегрировании учтено фильтрующее свойство δ-функции).

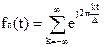
Спектральная плотность периодической функции

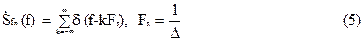определяется суммой δ-функций:

С учетом (5) интегрирование (4) дает результат (3). Из спектра (3) можно без искажений восстановить спектр Ś_x(f), следовательно, и сам непрерывный сигнал x(t) только при условии, если отдельные копии спектра Ś_x(f-kF_д) взаимно не пересекаются (см. предыдущий рис.). Это возможно, если F_д > 2F_в (или Δ < 1/2F_в). Восстановление осуществляют фильтром нижних частот, АЧХ которого показана на предыдущем рисунке пунктирной линией. Реализация такого фильтра тем проще, чем сильнее выполняется неравенство F_д > 2F_в.

Спектр дискретного сигнала можно определить не только по формуле (3), но и путем непосредственного применения прямого преобразования Фурье к функции (1). Это дает следующий результат:

Определим теперь спектр Фурье дискретного финитного

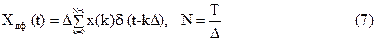(непериодического) сигнала, определенного на интервале (0;Т). Такой финитный сигнал можно записать в виде:

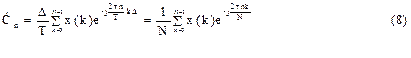Спектр сигнала (7) можно найти, если его периодически продолжить направо и налево с периодом Т. Тогда получаем периодический сигнал Х_{д пер}(t) совпадающий с Х_дф(t) на интервале (0;Т), для которого комплексные амплитуды Ćn можно получить из (6) при ω=2πn/Т суммированием от k=0 до k=N-1 и с учетом сомножителя 1/Т:

Формула (8) определяет коэффициенты дискретного преобразования Фурье (ДПФ). Из нее следует, что при заданных N отсчетах x(k) существует N коэффициентов ДПФ (n=0,1,2,3,…,N-1). Коэффициент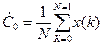

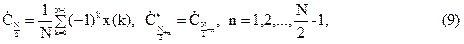определяет постоянную составляющую. При четном N из (8) следует для вещественных x(k):

т.е. коэффициенты ДПФ, номера которых располагаются симметрично относительно N/2, образуют комплексно-сопряженные пары. Можно считать, что коэффициенты ĆN/2, ĆN/2+2,…CN-1 соответствуют отрицательным частотам. Число же амплитуд, образующих спектр ДПФ равно N/2. Это следует из теоремы отсчетов Котельникова при Δ=1/2F_в. При таком условии спектр x_дпер(t) содержит F_в/(1/Т)=Т(2Δ)=N/2 амплитуд.

При заданных Ćn (n=0,1,2,3,…N-1) функцию x(k) можно определить с помощью обратного преобразования Фурье (ОДПФ), представляя периодическую функцию x_пер(t) c периодом Т рядом Фурье: